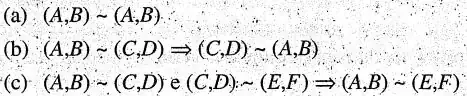1

I have the following laws:

enter image description here

And I did the following:

  • $(A,B)\sim(P,Q)\wedge (C,D)\sim (P,Q) \stackrel{?}{\implies} (A,B)\sim (C,D)$
  • $(A,B)\sim(P,Q)\wedge \stackrel{symmetry}{(P,Q)\sim (C,D)}\stackrel{?}{\implies} (A,B)\sim (C,D)$
  • $(A,B)\sim(P,Q)\wedge (P,Q)\sim (C,D) \implies (A,B)\sim (C,D)$

I guess this is it. Am I missing something? Also, is transitivity actually needed? It seems to be only a variant of symmetry, I guess that only symmetry is needed to show transitivity but I may be wrong.

Red Banana
  • 23,956
  • 20
  • 91
  • 192

1 Answers1

2

\begin{align} (A,B) \sim (P,Q) \text{ and } (C,D) \sim (P,Q) & \overset{(b)}\implies (A,B) \sim (P,Q) \text{ and } (P,Q) \sim (C,D) \\ & \overset{(c)}\implies (A,B) \sim (C,D) \end{align} In general, transitivity can't be shown from symmetry, see here.

Community
  • 1
desos
  • 2,929