Principal component analysis - calculating variance

Question

Quoting Rahul's answer:

It's not hard to show that if the covariance matrix of the original data points $x_i$ was $\Sigma$, the variance of the new data points is just $u^{T}\Sigma u$.

The covariance between sets $X$ and $Y$ is defined as $\sum_i = \frac{1}{n}(x_i-\bar{x})(y_i-\bar{y})$, where $\bar{x}$ and $\bar{y}$ denote the mean.

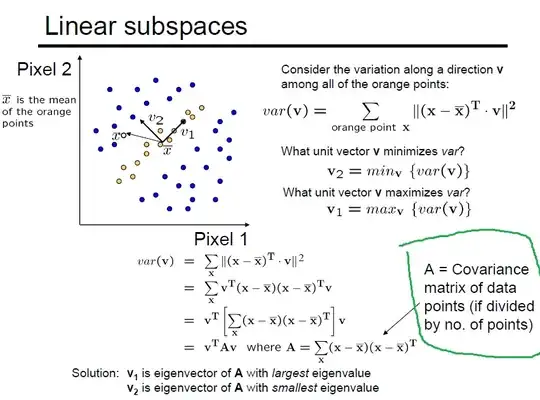
In some other material I've found it says something else than what I've quoted: Here, the variance is not equal to $u^{T}\Sigma u$. It would be if $A$ in this case were multiplied by $\frac{1}{n}$. They say $A$ would be a covariance matrix if the coefficient was present. But it's not. It looks 'a bit' incompatible with the statement in the quote.

The question is - who is wrong here and what is variance equal to? I suppose Rahul is right saying that the variance is equal to $u^{T}\Sigma u$, where $\Sigma$ is the covariance matrix. But the picture below proves a different equality, so what's going on here?

Here on page 8, the author derives the equality supporting Rahul's claim (I can't quite understand what's going on there). Which one is correct?

Source

Answer 1

Let $x_1,\dots,x_n\in\mathbb R^d$ be the set of sample points you are dealing with. Projecting onto a unit vector $v\in\mathbb R^d$ you get the samples $z_i := x_i^Tv\in\mathbb R$ for $i=1,\dots,n$. The sample mean of this list of numbers is $$ \overline z = \frac{1}{n} \sum_i z_i = \frac{1}{n} \sum_i x_i^T v = \left(\frac{1}{n} \sum_i x_i^T\right) v = \overline x^Tv, $$ where $\overline x = \frac{1}{n} \sum_i x_i$ is the sample mean of the unprojected data. Now the sample variance of the projected data is, by definition \begin{align*} \sigma_z^2 &= \frac{1}{n} \sum_i \left(z_i-\overline z\right)^2 \\ &= \frac{1}{n} \sum_i \left(x_i^Tv-\overline x^Tv\right)^2 \\ &= \frac{1}{n} \sum_i \left(\left(x_i-\overline x\right)^Tv\right)^2. \end{align*}

Note that what is called "$var(\mathbf v)$" in the slide you attached is not the sample variance $\sigma_z^2$, since the factor of $\frac{1}{n}$ is missing.

Hence, the two statements are not in conflict.

We can go on and obtain the result Rahul suggested: \begin{align*} \sigma_z^2 &= \frac{1}{n} \sum_i \left(\left(x_i-\overline x\right)^Tv\right)^2 \\ &= \frac{1}{n} \sum_i \left(x_i-\overline x\right)^Tv \left(x_i-\overline x\right)^Tv \\ &= \frac{1}{n} \sum_i v^T \left(x_i-\overline x\right) \left(x_i-\overline x\right)^Tv \\ &= v^T \left(\frac{1}{n} \sum_i \left(x_i-\overline x\right) \left(x_i-\overline x\right)^T \right) v = v^T \Sigma_x v, \end{align*} where $$\Sigma_x = \frac{1}{n} \sum_i \left(x_i-\overline x\right) \left(x_i-\overline x\right)^T$$ is the sample covariance matrix of the unprojected data.