Showing that this sum is equal to the fibonacci numbers

Question

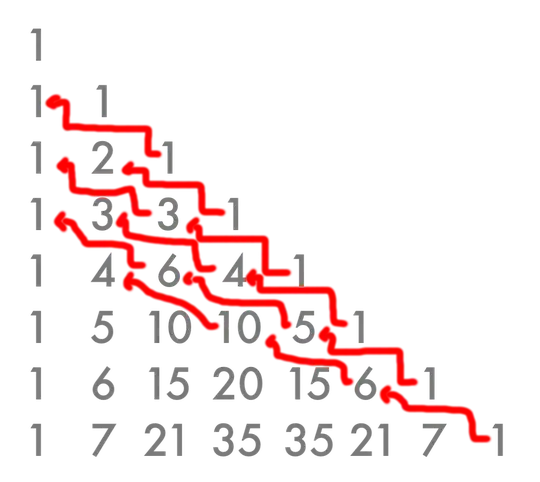
How do I show that the following sum is equal to the fibonacci numbers? Atleast numerical evaluation suggests it is $$ \sum_{k=0}^{\lceil n/2\rceil}\binom{n+1-k}{n+1-2k} $$ The image below shows how it moves through pascals triangle, it starts at the right $1$ on line $n+1$, if the upper line is $n=0$. enter image description here

Use induction, showing that your formula satisfies the Fibonacci recurrence relation $F(n+1) = F(n) + F(n-1)$. — Bob Krueger, Apr 05 '15 at 19:52
It may be easy to show that the relation is true, but it does not make the identity obvious. Take a look at the last picture here. — Bob Krueger, Apr 05 '15 at 20:03

score 3 · Accepted Answer · edited Apr 13 '17 at 12:21

3

It's clear that: $$ \binom{n+1-k}{n+1-2k}=\binom{n+1-k}{k} $$ and there is a solution here

edited Apr 13 '17 at 12:21

Community

1

answered Apr 05 '15 at 20:01

Elaqqad

13,725

Showing that this sum is equal to the fibonacci numbers

1 Answers1