7

I know that $x e^x = e$ means $x = 1$, but how do you solve for it?

TMM
  • 9,976

4 Answers4

26

If you want to prove the proposition that if $x e^x = e$ then $x = 1$, one way to do it is to just show that (1) $x = 1$ is indeed a solution of $x e^x = e$ by plugging the value in, and that (2) $x = 1$ is the only solution, for which you can argue that $x e^x$ is an increasing function on $x \ge 0$, and the equation clearly has no solution for $x < 0$.

If that makes it sounds like you have to know the answer beforehand before you can solve for it, well, that's not far from the truth. In general, if the right-hand side is an arbitrary real number $y$ instead of $e$, then you cannot solve $x e^x = y$ for $x$ in terms of elementary functions. One in fact defines the Lambert W function as precisely the solution of this equation.

  • 1
    1 is the only real solution, yes, but remember that the Lambert function is multivalued like the logarithm. (For those with Mathematica: N[ProductLog[Range[-5, 5], E]] and then Chop[E - % Exp[%]]) – J. M. ain't a mathematician Nov 28 '10 at 12:44
  • So guys, correct me if I am wrong: In many ways we can prove that x = 1, but given "xexp(x) = e", it is impossible to solve for x, that is, derive and write x = {some formula} = ... = 1. –  Nov 28 '10 at 21:33
  • 1
    @Perfecto: Not "impossible"; the reason the Lambert function was constructed so that it becomes possible! – J. M. ain't a mathematician Nov 28 '10 at 22:49
19

Another way is thinking of this as asking where do the graphs of the functions given by $f(x) = e^{x-1}$ and $g(x) = \frac{1}{x}$ intersect. This is because $$ xe^{x} = e \Leftrightarrow e^{x-1} = \frac{1}{x} \quad \text{for $x \neq 0$}$$ Then the answer you have would correspond to the only intersection point $(1, 1)$. So if you have no idea of where to start you could just draw the corresponding graphs and that could give you an idea of what is happening.

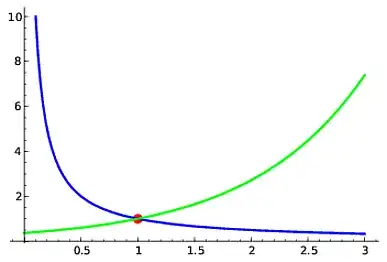
alt text

Then the graphs maybe would suggest to you the following line of reasoning. If $0 < x < 1$ then $$ \frac{1}{x} > 1 \quad \text{but} \quad e^{x-1} < e^{0} = 1$$ so their graphs can't meet in the interval $]0, 1[$. Then if $x > 1$ we have $$\frac{1}{x} < 1 \quad \text{but} \quad e^{x-1} > e^{0} = 1$$ so again there's no intersection point in the interval $]1, \infty[$.

This rules out all the possible solutions apart from $x = 1$ which you already knew and which could be guessed by looking at the graphs.

Adrián Barquero
  • 15,124
7

With logarithms.

Firstly $x>0$, Then :

$xe^{x}=e \Rightarrow \ln (xe^{x})=\ln e \Rightarrow \ln x + x = 1 $.

So:

If $x>1$ then $ \ln x >0$, thus $\ln x +x > 1+0 =1$ (contradiction)

If $x<1$ then $ \ln x < 0$, thus $\ln x +x < 1+0 =1$ (contradiction)

Thus $x=1$

Bryan Yocks
  • 2,271
3

Assuming that we are only looking for real solutions,

$$xe^x = e.$$

Note that $e^x$ is always positive and so no solution for this equation is possible for $x<0$ or $x=0$. As x increases, both x and $e^x$ are strictly increasing. Therefore, there is only one value for which $xe^x = e$. We already know that solution to be $x=1$.

Henry B.
  • 2,028