Limit of $\arctan(x)/x$ as $x$ approaches $0$?

Question

Quick question:

I came across the following limit: $$\lim_{x\rightarrow 0^{+}}\frac{\arctan(x)}{x}=1.$$ It seems like the well-known limit: $$\lim_{x\rightarrow 0}\frac{\sin x}{x}=1.$$ Can anyone show me how to prove it?

Answer 1

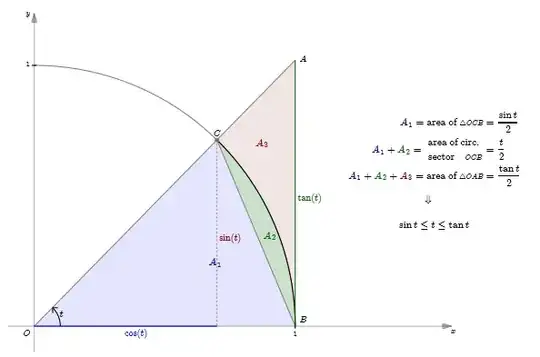
Recall (see the diagram below) that for $0\le t<{\pi\over2}$:

$$\tag{1} \sin t \le t \le \tan t. $$ Taking $t =\arctan x$ in $(1)$, we have, for $x>0$: $$ \sin\bigl(\arctan(x)\bigr)\le \arctan(x)\le x. $$ But $$ \sin\bigl(\arctan (x)\bigr) ={x\over \sqrt{1+x^2}}; $$ whence, for $x>0$: $$ {x\over \sqrt{1+x^2}}\le \arctan(x)\le x. $$ So, for $x>0$, we have $$ {1\over \sqrt{1+x^2}}\le {\arctan(x)\over x}\le 1; $$ and it follows from the Squeeze Theorem that $$ \lim_{x\rightarrow0^+} {\arctan(x)\over x}=1. $$

---

Answer 2

$$\lim_{x\rightarrow 0^{+}}\frac{\arctan(x)}{x}= \lim_{h\rightarrow 0^{+}}\frac{\arctan(0+h) -\arctan(0)}{h} = \arctan'(0) = \frac{1}{1+0^2} = 1$$

Answer 3

If you don't yet have access (which is often the case) to such relatively advanced tools as derivatives, L'Hopital's rule, and series expansion, here is a very simple proof:

Once you know:

$$\lim_{x \rightarrow 0} \frac{\sin x}{x}= 1$$

You can prove that

$$\lim_{x \rightarrow 0} \frac{\tan x}{x}= 1$$

Indeed,

$$\lim_{x \rightarrow 0} \frac{\tan x}{x}= \lim_{x \rightarrow 0} \frac{\sin x}{x \cdot \cos x}= \lim_{x \rightarrow 0} \frac{\sin x}{x} \lim_{x \rightarrow 0} \frac{1}{\cos x}= 1\cdot1 = 1$$

Now you make a simple substitution:

$$t = \arctan x \implies x = \tan t$$

$$x \rightarrow 0 \implies t \rightarrow 0$$

Finally,

$$\lim_{x \rightarrow 0} \frac{\arctan x}{x} = \lim_{t \rightarrow 0} \frac{t}{\tan t} = 1$$ (the last limit equals $1$, as proved above).

If you were actually looking for the proof $\lim_{x \rightarrow 0} \frac{\sin x}{x} = 1$ then there are plenty of nice unit circle proofs on the internet. Maybe you could try this one.

Answer 4

Let $x=\tan(\theta)$. Since $\lim\limits_{x\to0}\arctan(x)=0$, as $x\to0$, we also have $\theta=\arctan(x)\to0$. Thus, $$ \lim_{x\to0}\frac{\arctan(x)}{x}=\lim_{\theta \to0}\frac{\theta}{\tan(\theta)}\tag{1} $$ and $(1)$ is shown to be $\frac11$ in equation $(5)$ of this answer.

Answer 5

We can make use of L'Hopital's rule. Since $\frac{d}{dx}\arctan x=\frac{1}{x^2+1}$ and $\frac{d}{dx}x=1$, we have $$\lim\limits_{x\to0^+}\frac{\arctan x}{x}=\lim\limits_{x\to0^+}\frac{1}{x^2+1}=1.$$

Answer 6

Can you do the Taylor series' expansion of $\arctan (x)$? If you can, then it is easy to solve your limit. If you cannot, refer to this.

Answer 7

If you know that $\tan x \underset{x \rightarrow 0}{\sim} x $ you could compute :

$x = \arctan(\tan x) \underset{x \rightarrow 0}{\sim} \arctan x$ and then $ \frac{\arctan x}{x} \underset{x \rightarrow 0}{\rightarrow} 1$

Edit : sorry I don't see the proof above which use the same idea.