I needed the PI constant in C++, and I was lead to the answer that:
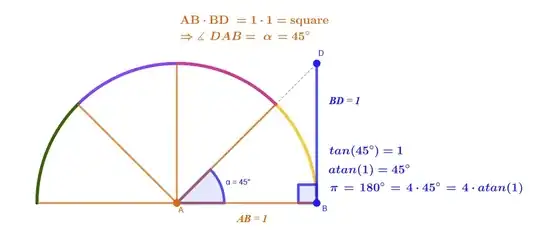
const PI = atan(1) * 4
Note that despite involving code, I'm asking this from a mathematics perspective.
I have 2 questions about this:
- Is this an estimation of PI, or should it give me a large degree of accuracy?
- How does this give PI?
On the second point, if I understand atan correctly, it takes a ratio of two sides, and returns the corresponding angle.
That means that atan(1) is referring a situation with 2 equal length sides.
I think I'm misunderstanding something though, as atan(1) gives me 0.7853981633974483, which seems like a very tiny angle.
If anyone can fill in the holes, it would be greatly appreciated.
pi = acos(-1)in C++, as I consider it neater. – GFauxPas Mar 29 '15 at 17:31const pi=3.1415926535897932384626433, but that's mostly because I cannot remember to simply use the predefineM_PI(cf. this) – Hagen von Eitzen Mar 29 '15 at 17:32atan(1) * 4overacos(-1)? – Leonardo Castro Sep 06 '16 at 14:17