Number of algebraic solutions to a formula related to a square tiling problem

Question

How can many different sets of prime-factors fit together so well in this formula?

I am curious about the number of solutions to the following equation:

$$ r_3 = \sqrt{2}\; \frac{ 1 + r_1 (r_2 -\sqrt{2} )} { 2 + \sqrt{3} - r_2 \sqrt{2}\; (1 + \sqrt{3}) + r_1 (2 + \sqrt{3}) (r_2- \sqrt{2}) } \tag {1} $$ where the $r_i$ are of the form $$ r_i = \sqrt{2}\; \frac{a_i-b_i\sqrt{3}} {c_i} \qquad i \in \{1,2,3\} \tag{2} $$ with {a, b, c} $\in$ $\mathbb N$ (positive Integers) and $r_i > \sqrt{2}$ .

This question is closely related to this one, because eq $(1)\,$ has a geometrical interpretation: All solutions with $ r_i > \sqrt{2} \;$ represent possible tilings of a square with similar copies of $\{45°,60°,75°\}$ triangles, and the $r_i$ are the ratios of base to side of trapezoids (formed by the triangles):

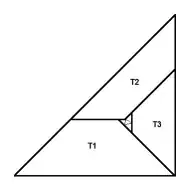
There are at least 37 solutions from $(1)$ (which represent unique tilings of a square with less than 100 triangles) like this for example:

$$ \begin{align} & \{\; r_1 = \sqrt{2}\; \frac{6-\sqrt{3}} {3} \;, \qquad \quad r_2 = \sqrt{2}\; \frac{13-3\sqrt{3}} {4} \;, \qquad \; \, r_3 = \sqrt{2}\; \frac{21-2\sqrt{3}} {15} \; \} \; ,\\ & \{\; r_1 = \sqrt{2}\; \frac{213-41\sqrt{3}} {66} \;, \qquad r_2 = \sqrt{2}\; \frac{49-9\sqrt{3}} {46} \;, \qquad \; \; r_3 = \sqrt{2}\; \frac{83-2\sqrt{3}} {46} \; \} \; ,\\ & \{\; r_1 = \sqrt{2}\; \frac{1689-419\sqrt{3}} {624} \;, \qquad r_2 = \sqrt{2}\; \frac{81-14\sqrt{3}} {33} \;, \qquad r_3 = \sqrt{2}\; \frac{170-21\sqrt{3}} {109} \; \} \; ,\\ & \{\; r_1 = \sqrt{2}\; \frac{1524-287\sqrt{3}} {654} \;, \qquad r_2 = \sqrt{2}\; \frac{1701-217\sqrt{3}} {759} \;, \qquad r_3 = \sqrt{2}\; \frac{499-52\sqrt{3}} {359} \; \} \; ,\\ & \dotsb \\ & \{\; r_1 = \sqrt{2}\; \frac{7545-1163\sqrt{3}} {3174} \;, \qquad r_2 = \sqrt{2}\; \frac{5-\sqrt{3}} {2} \;, \qquad r_3 = \sqrt{2}\; \frac{907-122\sqrt{3}} {661} \; \} \qquad \\ \end{align} $$

I don't know if i am completely missing something very basic here, but if the accumulation of many solutions to eq $(1)$ is not happening by pure chance, there has to be a mathematical reason for this.
I would have thought that it is very unlikely that many different prime-factors fit together simultaneously.

$\mathbf{Edit:}$

The only other expression (=trapezoid-setup) among many, for which i found geometrically interpretable solutions (with $r_i > \sqrt{2}$ ) is $ r_3 = \frac{ \sqrt{3}(7 \; r_2 - \sqrt{2} - 5\sqrt{3} \; r_2 + \sqrt{6})+2\sqrt{2} \; r_1 (r_2 + 2\sqrt{2} - \sqrt{6}) } {\sqrt{2} (7r_2 \; + \sqrt {6}- \sqrt{2}\;r_1 ( r_2 (1 + \sqrt{3})-( \sqrt{2}( \sqrt{3}-1) )) ) } \tag {3} $ which again has several valid geometric solutions corresponding to square-tilings with less than 100 triangles, including this one: $ r_1,_2,_3 = \{ \sqrt{2} (7851-1355 \sqrt{3})/3666\;, \sqrt{2} (106-7 \sqrt{3})/65\;, \sqrt{2} (5349 - 709 \sqrt{3})/2442 \} $ representing trapezoids consisting of 15, 13 and 15 triangles respectively.

The simplest solution of $(3)$ looks like this:

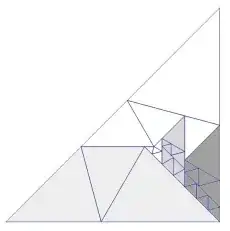
So it seems to be the case that although expressions like $(1)$ or $(3)$ have indeed an infinite number of general algebraic solutions, the $r_i>\sqrt2$ condition and other yet unknown requirements seem to allow valid geometric solutions only for a few cases with spezial trapezoid-arrangement and a finite number of solutions.

Answer 1

I'd say you have an infinite number of possible solutions.

I'd consider $a_i,b_i\in\mathbb Q$, i.e. my $a_i$ would be your $a_i/c_i$ and my $b_i$ would be your $b_i/c_i$. Then your equation $(1)$ can be rewritten such that it takes the form $P_1\sqrt6 + P_2\sqrt2=0$ where $P_1$ and $P_2$ are polynomials with rational coefficients in the six indeterminates $a_1,b_1,a_2,b_2,a_3,b_3$. The variety described by $P_1=0,P_2=0$ has dimension $4$, so you don't have a few distinct solutions, but a whole multidimensional variety of solutions.

If you want to know, the polynomials in question are

$$P_1 = 2 a_{1} a_{2} a_{3} - 4 b_{1} a_{2} a_{3} - 4 a_{1} b_{2} a_{3} + 6 b_{1} b_{2} a_{3} - 4 a_{1} a_{2} b_{3} + 6 b_{1} a_{2} b_{3} + 6 a_{1} b_{2} b_{3} - 12 b_{1} b_{2} b_{3} + 2 b_{1} a_{2} + 2 a_{1} b_{2} - 2 a_{1} a_{3} + 4 b_{1} a_{3} - 2 a_{2} a_{3} + 2 b_{2} a_{3} + 4 a_{1} b_{3} - 6 b_{1} b_{3} + 2 a_{2} b_{3} - 6 b_{2} b_{3} - 2 b_{1} + a_{3} - 2 b_{3}$$

and

$$P_2 = 4 a_{1} a_{2} a_{3} - 6 b_{1} a_{2} a_{3} - 6 a_{1} b_{2} a_{3} + 12 b_{1} b_{2} a_{3} - 6 a_{1} a_{2} b_{3} + 12 b_{1} a_{2} b_{3} + 12 a_{1} b_{2} b_{3} - 18 b_{1} b_{2} b_{3} - 2 a_{1} a_{2} - 6 b_{1} b_{2} - 4 a_{1} a_{3} + 6 b_{1} a_{3} - 2 a_{2} a_{3} + 6 b_{2} a_{3} + 6 a_{1} b_{3} - 12 b_{1} b_{3} + 6 a_{2} b_{3} - 6 b_{2} b_{3} + 2 a_{1} + 2 a_{3} - 3 b_{3} - 1$$

As you can see, these are linear in each of the indeterminates. So if you choose rational values for four of the six, you are left with a $2\times 2$ linear system of equations, again with rational coefficients. This leads to a unique rational solution. So for any rational choice of four of the variables, the remaining two will be rational as well.

Your extra conditions of $a_i,b_i>0$ and $r_i>\sqrt2$ rule out some of the solutions, but since it apparently still leaves a fair number of solutions, I feel confident that there still should be an infinite number of rational solutions left. In essence you are taking the intersection of $6$ half-spaces in $\mathbb Q^4$ and since that intersection evidently isn't just a single point (since you know of more than one solution), it has to contain an infinite number of rational points.

If you want to go back to your formulation with integers, you might homogenize my polynomials to

$$P_1' = 2 a_{1} a_{2} a_{3} - 4 b_{1} a_{2} a_{3} - 4 a_{1} b_{2} a_{3} + 6 b_{1} b_{2} a_{3} - 4 a_{1} a_{2} b_{3} + 6 b_{1} a_{2} b_{3} + 6 a_{1} b_{2} b_{3} - 12 b_{1} b_{2} b_{3} + 2 b_{1} a_{2} c_{3} + 2 a_{1} b_{2} c_{3} - 2 a_{1} c_{2} a_{3} + 4 b_{1} c_{2} a_{3} - 2 c_{1} a_{2} a_{3} + 2 c_{1} b_{2} a_{3} + 4 a_{1} c_{2} b_{3} - 6 b_{1} c_{2} b_{3} + 2 c_{1} a_{2} b_{3} - 6 c_{1} b_{2} b_{3} - 2 b_{1} c_{2} c_{3} + c_{1} c_{2} a_{3} - 2 c_{1} c_{2} b_{3}$$

and

$$P_2' = 4 a_{1} a_{2} a_{3} - 6 b_{1} a_{2} a_{3} - 6 a_{1} b_{2} a_{3} + 12 b_{1} b_{2} a_{3} - 6 a_{1} a_{2} b_{3} + 12 b_{1} a_{2} b_{3} + 12 a_{1} b_{2} b_{3} - 18 b_{1} b_{2} b_{3} - 2 a_{1} a_{2} c_{3} - 6 b_{1} b_{2} c_{3} - 4 a_{1} c_{2} a_{3} + 6 b_{1} c_{2} a_{3} - 2 c_{1} a_{2} a_{3} + 6 c_{1} b_{2} a_{3} + 6 a_{1} c_{2} b_{3} - 12 b_{1} c_{2} b_{3} + 6 c_{1} a_{2} b_{3} - 6 c_{1} b_{2} b_{3} + 2 a_{1} c_{2} c_{3} + 2 c_{1} c_{2} a_{3} - 3 c_{1} c_{2} b_{3} - c_{1} c_{2} c_{3}$$

but since you can't argue that an integral system of equations will lead to an integral solution, I prefer the rational approach here.