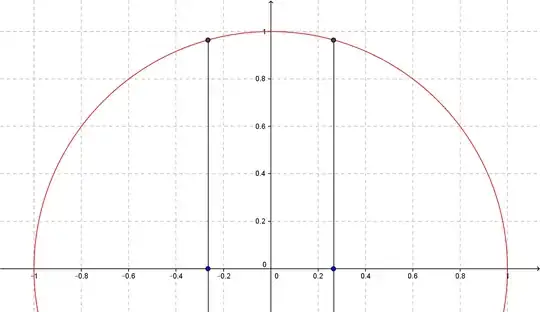
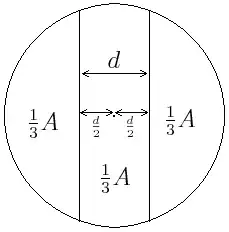
When I was young I came up with a geometry problem and drew it in a notebook:
Suppose we have a circle with radius $r$ and area $A$. Let two parallel lines be equidistant from the center of the circle and divide the circle's area into thirds. What is the distance $d$ between these two lines?
(Note: the following work contains the laughable mistake of solving $\int \sqrt{x^2-r^2} \; dx$ instead of $\int \sqrt{r^2-x^2} \; dx$. I'll go ahead and leave my work anyway:)
Later on, in high school, I found the notebook again and used my new calculus tools to approach the problem, which I recorded on the next few pages of that notebook. I recognized that $$\frac{1}{12}A=\frac{1}{12}(\pi r^2)=\int_0^{d/2} \sqrt{x^2-r^2}\; dx$$ $$=\frac{x}{2}\sqrt{x^2-r^2}-\frac{r^2}{2}\ln \left|x+\sqrt{x^2-r^2}\right|\biggl|_0^{d/2}$$ $$= \frac{d}{4}\sqrt{\frac{1}{4}d^2-r^2} -\frac{r^2}{2}\left[ \ln\left|{\frac{d}{2}+\sqrt{\frac{1}{4}d^2-r^2}} \right| -\ln\left|\sqrt{-r^2} \right| \right] $$ But we know that $$\frac{1}{4}d^2-r^2<0$$The final equation I wrote down was $$r^2= \frac{3d}{\pi}i\sqrt{r^2-\frac{1}{4}d^2} -\frac{6r^2}{\pi}\left[ \ln\left|{\frac{d}{2}+i\sqrt{r^2-\frac{1}{4}d^2}} \right| -\ln\left|ir\right| \right] $$ and this is where I probably slammed the notebook shut in frustration.
I'm more mathematically mature now (college student) and want to finally get an answer to this problem. There are probably a few different ways to approach this problem. I found a version of this problem on MSE here, but mine is the particular case $n=2$. Can anybody help me put this decade-old problem to rest? I mainly posted this because I want to know if there is some elegant solution out there to this seemingly simple problem (e.g. solution without numerical methods).