Fundamental unit in the ring of integers $\mathbb Z[\frac{1+\sqrt{141}}{2}]$

Question

Find a fundamental unit in the ring of integers $\mathbb Z[\frac{1+\sqrt{141}}{2}]$ of $\mathbb Q(\sqrt{141})$

I have different corollaries for different numbers, the most appropriate for $141$ is the one below.

I used an algorithm (don't know if you know this, but

$\beta_0=\sqrt{141}+\lfloor\sqrt{141}\rfloor, \quad\beta_{n+1}=\frac{1}{\beta_n-\lfloor\beta_n\rfloor}$

$a_n=\lfloor\beta_n\rfloor$

$p_n=p_{n-1}a_n+p_{n-2}, \quad q_n=q_{n-1}a_n+q_{n-2} $) to determine the continued fraction expansion of $\sqrt{141}$

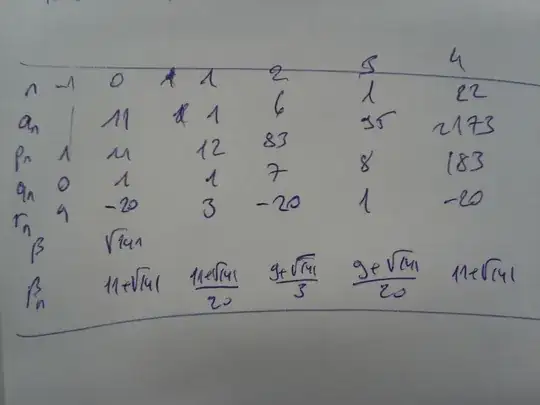
As you see the the sequence $(\beta_n)_n$ is periodic with period $t=3$ and thus $\sqrt{141}=[11;\overline{1, 6, 1, 22}]$, and $\pm4$ doesn't appear in the sequence $r_0,\dots,r_{t-2}$, so according to the corollary can I then assume that the fundamantel unit is also the fundamental solution, i.e. $95+8\sqrt{141}$ ?

Answer 1

$\sqrt{141}=[11,\overline{1,6,1,22}]$. Yes $95+8\sqrt{141}$ is a fundamental unit.

Answer 2

Proposition 19 says we need to check a few things:

• $141 > (\pm 4)^2 + \frac{1}{2}(|\pm 4| + 1)$
• Then $x^2 - 141y^2 = \pm 4$ appears as solution to continued fraction expansion to $\sqrt{141}$.

Since $\pm 4$ does not appear in your remainders, $x^2 - 141 y^2 = \pm 4$ does not have a solution. Therefore you just solve Pell equation with $r = 1$, which is guaranteed to happen by Propoisition 2.20

Alternatively, Pell's equation says we can approximately find the square root of $141$:

$$ \left| \frac{x}{y} - \sqrt{141} \right| = \frac{4}{y^2}\cdot \frac{1}{\sqrt{\tfrac{4}{y^2} +141 }+ \sqrt{141}} \color{red}{\mathbf{<}} \frac{1}{2y^2}$$

The red inequality is not always true if $(4,141)$ is replaced with $(r,d)$, so we make up this condition as part of the theorem, so ensure the error is small enough to be a continued fraction.

---

The existence of Fundamental unit has to do with the Pigeonhole Principle. In fact, it was used in several places. Here is one.

Some integer $r \in \mathbb{Z}$ must have infinitely many solutions to the Generalized Pell Eq

$$ x^2 - dy^2 = r $$

Then we can take two such solutions (congruent mod $r$) and divide them and observe we still have element of $\mathbb{Z}[\sqrt{d}]$.

$$ x + y\sqrt{d} = \frac{x_1 + y_1\sqrt{d}}{x_2 + y_2\sqrt{d}} = \frac{(x_1 x_2 - d \cdot y_1 y_2)+ (x_1 y_2 + y_2 x_1)\sqrt{d}}{r} $$

This ratio is a solution to Pell equation $x^2 -d y^2 = 1$.