7

How can I find the value of the expression $\sqrt{2}^{\sqrt{2}^{\sqrt{2}^...}} $? I wrote a computer program to calculate the value, and the result comes out to be 2 (more precisely 1.999997). Can anyone explain what's happening? Is there any general method to calculate these expressions? I am new to these problems.Thanks in advance!

EDIT On looking at the answer by Clement C., I thought I could generalize the method to find the value of any expression of the form $\sqrt[n]{n}^{\sqrt[n]{n}^{\sqrt[n]{n}^...}} $. The value should be $n$, but this is not the case. This is the graph for $n<50$.

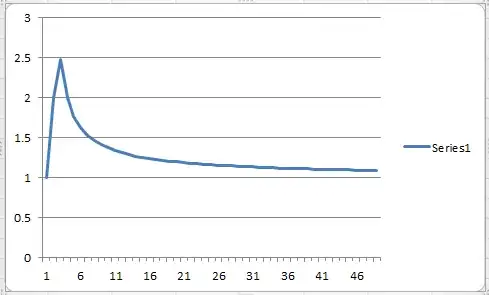
enter image description here

Any help would be appreciated.

JavaNewbie_M107
  • 171
  • 7
    $\sqrt2^x=x$ ... – WillO Mar 24 '15 at 14:50
  • 2
    This is called infinite tetration denoted by $^\infty a=\underbrace{a^{a^{a^{\ldots}}}}_{n\textrm{ times}}$ – Prasun Biswas Mar 24 '15 at 14:53
  • An important fact: $x^{x^{x^{\cdots}}}$ can never exceed $e$, which it achieves for $x=e^{1/e}$. In particular, the value for $x=3^{1/3}$ cannot be $3$. – Andrew Dudzik Mar 25 '15 at 04:48
  • http://math.stackexchange.com/questions/1089458/how-can-i-prove-the-convergence-of-a-power-tower – Bumblebee Mar 25 '15 at 05:29
  • For your more general method the limit should be 1. Just consider $\lim_{n \to \infty}\ n^{n^{-1}}$. – ThisIsNotAnId Mar 25 '15 at 06:40
  • If we let $S$ be the solution to the sum, then for a given $n$ we know that $S$ satisfies $\frac{\log(S)}{S} = \frac{\log(n)}{n}$. One solution to this is $n$ but notice this is not the only solution. For example $n=4$, both 2 and 4 satisfy the equation and the value you are seeing the convergence to in your graph is the solution $\leq e$. – rwolst Mar 25 '15 at 10:06
  • 1
    Note that if we have one solution $n$, the other can be found by equating $\frac{\log(n)}{n} = \frac{\log(n^k)}{n^k} = \frac{\log(n)}{(1/k) n^k}$ and solving $\frac{1}{k} = n^{1-k}$ for $k$. You can easily verify this for the 2,4 solution case. – rwolst Mar 25 '15 at 10:18

3 Answers3

20

We don't allow infinite expressions, so first you need to define what it means. One way to make sense of it is as a sequence, $a_1=\sqrt 2, a_2 =\sqrt 2 ^{\sqrt 2}, a_3=\sqrt 2 ^{\sqrt 2^{\sqrt 2}},a_n=\sqrt 2^{a_{n-1}}$ and ask if the sequence has a limit as $n \to \infty$ If the limit exists, call it $L$. Then $L=\sqrt 2^L$, which is satisfied by $2$. To prove the limit exists, show that $a_n \lt 2 \implies a_{n+1} \lt 2$ and $a_n \gt 1 \implies a_{n+1} \gt a_n$. The sequence is now monotone and bounded above, so has a limit.

Ross Millikan
  • 374,822
  • All this is also true for $L=4$: $4=\sqrt{2}^4$, $a_n \lt 4 \implies a_{n+1} \lt 4$. How would you rule $L=4$ out? – g.kov Mar 24 '15 at 18:01
  • @g.kov The only two real candidates for $L$ from the equation $L=\sqrt{2}^L$ are $2$, and as you noted, $4$. The sequence $a_n$ is bounded above by $2$, so $4$ cannot be the limit since $4>2$. Thus, the only remaining candidate for the limit is $2$. – Peter Olson Mar 24 '15 at 18:22
  • 1
    @Peter Olson: Perhaps, the answer of Clement C. is more complete, it depends on the initial value $a_1$. Why would we set $a_1=\sqrt{2}$? If we set $a_1=4$ then we get a constant sequence $a_n=4$. – g.kov Mar 24 '15 at 18:51
  • @g.kov: we set $a_1=\sqrt 2$ because that is the term with one $\sqrt 2$ in it and I was making the sequence so that term $a_n$ has $n\ \sqrt 2$'s – Ross Millikan Mar 24 '15 at 20:00
  • @g.kov Sure, $4$ is the limit of the sequence $a_n=4$, I'm sure everybody agrees with that, but it's not the limit of the sequence he defines in the answer with $a_1=\sqrt{2}$ and $a_n=\sqrt{2}^{a_{n-1}}$. I was talking about how to rule out the possibility $L=4$ from this sequence, not from some other sequence not mentioned in the answer. – Peter Olson Mar 24 '15 at 20:19
  • @Ross Millikan: There is no spacial in the value $\sqrt{2}$, we can start with e.g. $1$ or $2$, or $\mathrm{e}$, or $\pi$ with the same result $x=2$, or we can start it with $4$ and get $x=4$. The whole tower $\sqrt{2}^{\sqrt{2}^{\sqrt{2}^...}}$ object is not an expression that starts from $\sqrt{2}$ and unfolds infinitely down, as it may look. The equation $x=\sqrt{2}^{\sqrt{2}^{\sqrt{2}^...}}$ just has two real solutions as stated in the answer of Clement C., much like the equation $x^2=1$ has two real solutions $x=\pm1$. There is no reason to discriminate a second real solution here. – g.kov Mar 24 '15 at 21:15
  • I think the approach is good, but the confusion might be arising from not showing that 2 is the least upper bound. This way we also don't need to assume $L$ exists. – ThisIsNotAnId Mar 25 '15 at 03:37
  • 1
    @ThisIsNotAnId: The point is I don't have to show that 2 is a least upper bound. I have shown that it is an upper bound and that the sequence is monotonic, which proves there is a limit. I have excluded 4 as a limit because 2 is an upper bound. I have not shown that there is not another potential limit (which must be less than 2). That can be done, but I haven't done it. The idea of "starting with 4" is nonsense-I have defined a sequence and it starts with $\sqrt 2$. If someone wants to define another way of approaching this question, they are free to do so. – Ross Millikan Mar 25 '15 at 04:01
6

As WillO wrote, once properly defined as the limit of the recursive sequence $a_{n+1} = \sqrt{2}^{a_n}$ (which exists by monotonicity, for any initial value $a_0$), the value $x$ you are looking for satisfies the equation $$ \sqrt{2}^x =x $$ (can you see why?), or equivalently $$ \frac{\ln 2}{2} = \frac{\ln x}{x} $$ (by taking the logarithm and rearranging the terms). Clearly, $2$ is a solution (to this equation, that any solution $x$ to the original problem must in particular satisfy), as is $4$: to show that these are the only ones, observe that $x\mapsto \frac{\log x}{x}$ is increasing on $(0,1]$, and decreasing on $[1,\infty)$. Now, depending on the initial value $a_0$ of your sequence, the solution has to be one of the two. I assume you want $a_0=1$.

Clement C.
  • 67,323
  • 1
    I only stated that 4 could be a limit of the recursive sequence, from solving the equation (not that it was). Any solution must be in ${2,4}$. – Clement C. Mar 24 '15 at 15:04
  • You post says "Clearly, 2 is a solution, as is 4". To me that sounds that you claim it to be a valid solution. You may want to consider an edit. – mjnichol Mar 24 '15 at 17:41
  • @mjnichol: is it clearer now? (I added a sentence to make the distinction explicit). – Clement C. Mar 24 '15 at 17:46
  • @Prasun Biswas: $\large e^{e^{-1}}\approx 1.444667861\lt 2$. Are you suggesting that $x=2$ cannot be a solution? – g.kov Mar 24 '15 at 18:59
  • @g.kov, sorry, I made a small error in my comment. Editing it now! – Prasun Biswas Mar 24 '15 at 19:17
  • Damn, I can't edit it. Anyway, what I meant is that the infinite tetration $y=^\infty a$ can take values of $x$ only upto $x=e$ corresponding to the unique solution $y=e^{e^{-1}}$ at $x=e$. @g.kov – Prasun Biswas Mar 24 '15 at 19:18
  • +1 for dependence on the initial value. Perhaps the common misunderstanding is that since we see a lot of $\sqrt{2}$ we assume that this tower "starts" somewhere high at $a_1=\sqrt{2}$ and infinitely unfolds from there down. But this is not exactly true, it "starts" at any height with the limit value already, which equally can be 2 as well as 4. – g.kov Mar 24 '15 at 19:23
  • @Prasun Biswas: That what I thought it is. Then your comment is not relevant. Btw, you can delete it – g.kov Mar 24 '15 at 19:25
3

You can rewrite your expression as $$\sqrt2^{\sqrt2^{...}}=2^{(\frac{1}{2})^{2^{...}}}$$ Clearly multiplying the powers out you end up with $$2^{1^{1^{...}}}=2$$

adrug
  • 111
  • 3
    I don't quite follow your "clearly multiplying the powers out". – rwolst Mar 24 '15 at 20:04
  • @rwolst I think he means a^b^c = a^(bc) – bjb568 Mar 25 '15 at 02:35
  • I think this the best solution and also the best explanation. Tbh, I didn't really understand the other answers. – Neil Mar 25 '15 at 06:59
  • 1
    I don't think this is logically correct i.e. the second line doesn't immediately follow from the first and the fact that $(a^b)^c = a^{bc}$. (Instead see Clement's answer). For example if $f(k)$ represents $k$, $\sqrt{2}$'s in the expression can you use this method for $f(3)$ say? – rwolst Mar 25 '15 at 09:45
  • I agree the other two answers are clearer and this would not be a sufficient proof for a textbook, but it shows some intuition. You can't use the method for $f(3)$, but the question doesn't need you to - the expression has infinitely many terms. The question whether the total number of them is even or odd is not well defined, and you can clearly rewrite each consecutive two of them as $x^{(\frac{1}{2})^2}$ or, if you prefer, $x^{2^\frac{1}{2}}$, leaving you with an expression made of repeated $x^{1^1}$. – adrug Mar 25 '15 at 11:09
  • 1
    This is saying a^b^c = (a^b)^c = a^(bc), but I think the question is about a^(b^c). – David K Mar 25 '15 at 12:27
  • @adrug I was using $f(3)$ as an example to illustrate what is going wrong with your method and not to highlight any even or odd issue. Essentially, the terms aren't cancelling as clearly as you say they should be. – rwolst Mar 25 '15 at 13:43