Implicit line equation

Question

Trying to understand parametric and implicit line equations but I'm at a complete halt now. I have a line that goes through P(0,1) and Q(3,2), I need to find the implicit equation N((x,y)- Z) = 0 such that Z is a point on the line and N is a vector perpendicular to the line. Please point me in the right direction. Thank you.

Answer 1

Things you need to know to do this problem:

PARAMETRIC FORM

The parametric form of a line is given by $\mathbf r(t) = \mathbf r_0 + t\mathbf v$. Let's forget about the $\mathbf r_0$ for a second: $\mathbf r(t) = t\mathbf v$ is the set of all the points on the line that passes through the origin and the point $\mathbf v$. So we can see that $\mathbf v$ defines the direction of our line -- thus it is called a "direction vector" for the line (but remember, there are an infinite number of direction vectors for any line -- for instance, once you find a vector $\mathbf v$, then $2\mathbf v$ is ALSO a direction vector).

This is a plot of the line that passes through the origin and the point $(1,2)$, i.e. $(x,y) = t(1,2)$:

So then what does $\mathbf r_0$ do? It translates that line. Say you want the line which is parallel to the one given above, but which passes through the point $(-1,1)$, then the equation for it is just $(x,y) = (-1,1) + t(1,2)$. Here's the plot:

So to find the parametric form of the equation of a line you just need one vector (point) which represents the direction of the line -- I used $(1,2)$ in my example -- and one point on the line -- I used $(-1,1)$.

NOTE Your textbook may specify the parametric form as a set of scalar equations. That is exactly equivalent to as my vector equation above, just in a less compact form. In scalar form this second line would be $x=t-1$, $y=2t+1$. Can you see how this is exactly the same?

---

IMPLICIT FORM

Now, let's consider what you're calling the implicit form (I've never heard it called that, but I am very familiar with it nonetheless). An affine space (like lines and planes and such) given by $\mathbf n \cdot (\mathbf r-\mathbf r_0)=0$ will always be an $(n-1)$-dimensional space, where $n$ is the dimension of the ambient space. For instance, in your problem, you have a line specified in the Euclidean plane. A plane is $2$-dimensional and a line is $1$-dimensional, so we can represent your line via this formula.

Now, what is this formula actually saying? Well, first we need to remember the definition of orthogonality (perpendicularity). If $\mathbf a, \mathbf b \in \Bbb R^n$ (that is $\mathbf a$ and $\mathbf b$ are vectors (points)), then $\mathbf a\ \bot\ \mathbf b$ (this is the symbol for $\mathbf a$ is orthogonal to $\mathbf b$) if and only if $\mathbf a \cdot \mathbf b =0$. So this implicit formula clearly has to do with orthogonal vectors.

Let's consider the line passing through points $\vec a$ and $\vec b$ (I'm changing my notation so that it corresponds to this picture I found). Then clearly $\vec a - \vec b$ is a vector pointing in the direction of our line. See the picture here:

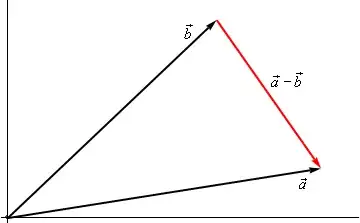
Now, what if instead of the vector $\vec a$, we just put $(x,y)$ -- which is some arbitrary point on our line. Then for $\vec b$ we could put in some specific point $(x_0, y_0)$ (where those would be filled in with numbers) on the line. Then if we had any vector orthogonal to our line, it would have to be orthogonal to $(x,y) - (x_0,y_0)$. So if we had such an orthogonal vector, it would completely specify the conditions that all $(x,y)$ must have to be on the line. Yay.

So let's see how to do it in the case of the line I gave you above (the one going through point $(-1,1)$ with direction vector $(1,2)$). Verify for yourself that an orthogonal vector to the direction vector $(1,2)$, is $(-2,1)$. Then we can just plug in: $\mathbf n \cdot (\mathbf r-\mathbf r_0)=(-2,1)\cdot((x,y)-(-1,1))=0$.

Now we've found the implicit form AND parametric forms for this line. Now can you find them for YOUR line?

Answer 2

Given the points: $$\begin{gathered} P(0,1) \hfill \\ Q(3,2) \hfill \\ \end{gathered}$$ Build the vector pointing from $P$ to $Q$: $$\overrightarrow {PQ} = Q - P = \left( {\begin{array}{*{20}{c}} 3 \\ 1 \end{array}} \right)$$ Set parametrization: $$\left( {\begin{array}{*{20}{c}} x \\ y \end{array}} \right) = P + t\overrightarrow {PQ} = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right) + t\left( {\begin{array}{*{20}{c}} 3 \\ 1 \end{array}} \right)$$ Observe that $$N = \left( {\begin{array}{*{20}{c}} { - 1} \\ 3 \end{array}} \right)$$ is orthogonal for $\left( {\begin{array}{*{20}{c}} 3 \\ 1 \end{array}} \right)$. With: $$\left( {\begin{array}{*{20}{c}} x \\ y \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right) = t\left( {\begin{array}{*{20}{c}} 3 \\ 1 \end{array}} \right)$$ we get from dot product: $$N \cdot \left( {\begin{array}{*{20}{c}} x \\ y \end{array}} \right) - N \cdot \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right) = t \cdot N \cdot \left( {\begin{array}{*{20}{c}} 3 \\ 1 \end{array}} \right)$$ so: $$ - x + 3y - 3 = 0$$

Now we set: $$f(x,y) = - x + 3y - 3$$ and verify:

$$\begin{gathered} f(P) = - 0 + 3 - 3 = 0 \hfill \\ f(Q) = - 3 + 6 - 3 = 0 \hfill \\ \end{gathered} $$ Function $f$ implicitly defines a line.

Answer 3

Let $\mathbf{V} = [ p_x - q_x; p_y - q_y ]$ be the vector that points from $P$ to $Q$. Then every point on the line is given by $\mathbf{P} + \alpha V$, $\alpha \in \mathbb{R}$. (You could also describe the line with $\mathbf{Q} + \alpha V$ or $\mathbf{Z} + \alpha V$; it doesn't matter as long as the point is on the line, but we know that $\mathbf{P}$ is, so we use it.) To find the vector orthogonal to the line, $\mathbf{N}$, use the dot-product with $\mathbf{V}$:

$$ \mathbf{N}^T \mathbf{V} = n_x v_x + n_y v_y = 0. $$

Can you take it from here?