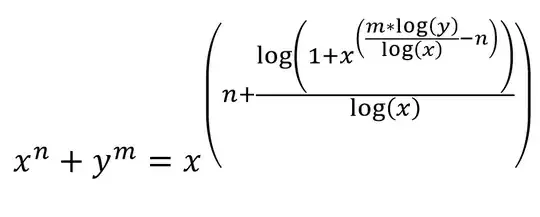3

Is there a rule for adding exponential terms of like bases just like there are rules for multiplying and dividing such terms?

For example we know that:

$x^1 \cdot x^2 = x^{1+2} = x^3$

But what about for addition (or subtract for that matter)?

$x^1 + x^2 = x^?$

If no such pattern exists, why is that?

jcelios
  • 1,181
  • only that you can factor out such an $x$. For example $x+x^2=x(x+1)$. – Holdsworth88 Mar 14 '12 at 16:41
  • 1
    In general, it’s fruitless to ask why some formulation or other is not true. Why? Because in mathematics, nothing is true at all, unless there’s a proof that it’s true. In mathematics, we don’t proceed from rules to examples, we proceed from examples to rules, in spite of the way students are being taught in schools. In this sense, mathematics is truly an experimental science. – Lubin May 09 '16 at 15:41
  • 2
    $$?=\log_x(x^1+x^2)$$ –  May 09 '16 at 15:45
  • @YvesDaoust Haha like really. !!! –  Feb 27 '18 at 16:52
  • For the record, I suggested an edit adding the tag "exponentiation", but it was rejected. – Later Jul 06 '23 at 09:46

5 Answers5

5

You can factor $x^1+x^2$ into $x(1+x)$, but it is not a power. There is no addition law for powers in the way you posit because positive integer powers equal repeated multiplication, not addition:

$$x^{n+m}=\underbrace{x\cdot x\cdot x\cdots x}_{n+m}=\underbrace{x\cdot x\cdots x}_n\cdot\underbrace{x\cdot x\cdots x}_m=x^{n}\cdot x^m.$$

However, the addition law would work for multiplication by integers, rather than integer powers:

$$(n+m)x=\underbrace{x+ x+ x\cdots x}_{n+m}=\underbrace{x+x\cdots x}_n \,+\, \underbrace{x+x\cdots x}_m =nx+mx.$$

Again, with $n+m$ a positive integer. There are conceptual quandries about repeated operations here that I will not go into, but suffice it to say these repetition formulas hold as valuable cases.

Community
  • 1
anon
  • 151,657
  • there is some kind of rule though. $$ 2^4 + 2^2 = 20 $$ $$ log_2(20) = 4.3219280949 $$ $$ 20 - 2^4 = 4 $$ $$ 2^.3219280949 = 1.25 = 5/4 $$ – William Oct 07 '14 at 03:01
2

Hint $\,\ x + x^2\, =\, x^n,\ \ n> 1\:$ has at most $\:n\:$ roots over a field (or domain) so it cannot possibly hold true for all elements in an infinite domain.

Bill Dubuque
  • 272,048
  • In what way does $x\cdot x^2=x^n$ differ ? –  May 09 '16 at 15:47
  • @YvesDaoust It differs only in that there is a value $,n = 3,$ where it becomes an equality of polynomials, i.e. their difference is the zero polynomial, which has infinitely many roots (every element) in an infinite domain. This cannot occur in the case in the answer. – Bill Dubuque May 09 '16 at 16:08
2

Observe that $ \log(A+B) = \log(A) + \log \left(\frac{B}{A} + 1 \right) $. Using this fact, one can show that $ \begin{align} \log (x^a + x^b) &= \log(x^a) + \log ( x^{b-a} + 1 ) \\ &= a\log x + \log ( x^{b-a} + 1 ) \\ &= \log x \left( a + \frac{\log ( x^{b-a} + 1 )}{\log x} \right) \\ \Rightarrow x^a + x^b &= x^{\left( a + \frac{\log ( x^{b-a} + 1 )}{\log x} \right)} \\ \text{In your case, with }& a=1, b=2, \text{ we get} \\ x^1 + x^2 &= x^{\left( 1 + \frac{\log ( x + 1 )}{\log x} \right)} \end{align} $

Will
  • 21
0

You can say that $x^1+x^2=x(x+1)$ or $x^a+x^b=x^a(1+x^{b-a})$ by the distributive law, but there is no $k$ such that $x^1+x^2=x^k$

Ross Millikan
  • 374,822
0

formula

I'm not sure what it's called or who discovered it, I just came across it.

hardmath
  • 37,015
Name
  • 1
  • 2
    In general you should cite your source ("I just came across it") and give an explanation. Otherwise it makes a fairly poor occasion for Readers to learn from what you write. – hardmath Jan 04 '16 at 15:20
  • 1
    @hardmath It was discovered by a youtuber called GradeAUnderA, he has said that he still has the paper but it isn't on arXiv or anything like that. He also says it is a pretty bad proof which might not actually be right. – Nico A Jan 05 '16 at 11:52
  • Seriously? Its not self-explanatory? It's not a unique result and I'd expect most readers here to be able to verify it for themselves. Just... do it. $x^n + y^m = x^m + x^{\log_x y}=x^m(1 + x^{\frac {\log y}{\log x}})=....$ etc. – fleablood Nov 27 '16 at 17:44