Evaluating Difficult Monte Carlo Integration in R

Question

I recently posted a simple version here (Simple Monte Carlo Integration).

I was able to verify that the answer was indeed close to 1/3 when I wrote the following R code, and got a mean of X of ~1/3:

U = runif(10000,0,1)
X = U^2
mean(X)

I am applying a more difficult Monte Carlo Integration now for two reasons. First, the integration is between 0 and infinity. Second, I believe the integration leads to gamma functions. What is the simplest way to approach the following problem, especially using a simple simulation as I did above (generating 10,000 uniform values and simulating in R):

$$\displaystyle \int_0^\infty \dfrac 34 x^4e^{-x^{3/4}}\,dx$$

I do not even know what value to expect (like I did in my previous post, where I knew my simulation should approximate 1/3). Even if I did, I do not know where I would use the 10000 uniform samples between 0 and 1, as this problem is now between 0 and infinity.

Answer 1

We are trying to use Monte Carlo Simulation to find:

$$\displaystyle \int_0^\infty \dfrac 34 x^4e^{-x^{3/4}}\,dx$$

As you have discovered, the infinite limits are problematic. We can do several things to overcome this

Approach 1: A naive approach is to plot the function given that it has a decaying exponential which tends to zero very quickly. If we plot this function, we see:

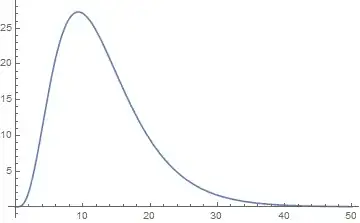
So, lets try to approximate it as:

$$\displaystyle \int_0^{50} \dfrac 34 x^4e^{-x^{3/4}}\,dx$$

Using your approach (recall, now your code needs to change to generate random numbers $(a, b)$ and with the function of interest) with $n = 10000$, we get:

$$I = 387.256$$

If we calculate the exact integral we get:

$$I = \Gamma \left(\frac{20}{3}\right) \approx 389.035$$

Approach 2: In this approach we will make a change in variables so as to map an infinite range of integration into a finite one.

A good example that works for functions that decrease towards infinity faster than $\frac{1}{x^2}$ is to use:

$$\displaystyle \int_a^b f(x)~dx = \int_{\frac{1}{a}}^{\frac{1}{b}} \dfrac{1}{t^2}f\left(\dfrac{1}{t}\right)~dt$$

With this altered approach, we can now do integrals when one of the limits is infinite and the other limit is of the same sign. If you need to integrate say something that has $a = 0$, what you do is break the integral into two parts and use Monte Carlo on each one.

If we have infinite limits for both limits, we could split the integral into three or more parts. So, for this problem, we have to split it into two pieces as:

$$\displaystyle \int_0^\infty \dfrac 34 x^4e^{-x^{3/4}}\,dx = \int_0^1 \dfrac 34 x^4e^{-x^{3/4}}\,dx + \int_0^1 \dfrac{1}{t^2} \left(\dfrac 34\right) \left(\dfrac 1t \right)^4 e^{{-(\frac 1t)}^{\frac 34}}~dt$$

Using the Monte Carlo for the first part, we get $I_1 = 0.0647226$ and for the second part, we get $I_2 = 387.551$, which yields:

$$ \displaystyle \int_0^\infty \dfrac 34 x^4e^{-x^{3/4}}\,dx = 387.616$$

Compare that to our previous and the exact result.

Approach 3: In this approach we will make a change in variables so as to map an infinite range of integration into a finite one. This time, we will transform variables using $u = \frac{1}{1+x}$, yielding:

$$\displaystyle \int_0^\infty \dfrac 34 x^4e^{-x^{3/4}}\,dx = \int_0^1 \frac{3 e^{-\left(\frac{1-u}{u}\right)^{3/4}} (1-u)^4}{4 u^6} ~ du$$

Running the Monte Carlo simulation with $n = 10000$ yields:

$$I = 390.18704821709946$$

Answer 2

One approach is to not sample uniformly on anything. This approach is nice because you can continue to get improved accuracy without having to restart the calculation to change the interval size.

The idea is importance sampling. Here there is a fairly easy importance sampling approach: you want something that has a factor of $e^{-x^{3/4}}$ and is also easy to integrate. If you had to analytically integrate something with a factor of $e^{-x^{3/4}}$, you would want a factor of $x^{-1/4}$ to serve as your "$du$". To this end, you can write your integral as

$$\frac{3C}{4} \int_0^\infty x^{17/4} \frac{e^{-x^{3/4}} x^{-1/4}}{C} dx$$

where $C=\int_0^\infty e^{-x^{3/4}} x^{-1/4} dx = \frac{4}{3}$. Having written this, we conclude that if $\xi$ has the density $\frac{e^{-x^{3/4}} x^{-1/4}}{C}$ then your integral is $\frac{3C}{4} \mathbb{E} \left [\xi^{17/4} \right ]=\mathbb{E}[\xi^{17/4}]$. Next the CDF of $\xi$ is just $e^{-x^{3/4}}$ for $x \geq 0$. Hence the quantile function (on the relevant range) is $Q(x)=\ln(1/x)^{4/3}$. Hence your integral is $\mathbb{E}[\ln(1/U)^{17/3}]$ where $U$ is uniformly distributed on $(0,1)$. (Note that this way of rewriting it has also exposed how to get the exact solution: $\ln(1/U)$ is Exp(1) distributed, so this is actually telling you that your original integral was $\Gamma(20/3)$.)

Notably this approach generates a lot of samples near $0$, where $x^{17/4}$ is small, but it should still work.

Also, given the $3/4$ in the original integral, I suspect that this approach was the one anticipated by the author of the question (since it cancels nicely with the normalization constant in this formulation).

Answer 3

Another approach is compute the integral by Gauss-Laguerre numerical integration, which is very suitable in this case:

$$\int_{0}^{\infty}\frac{3}{4}x^4e^{-x^{3/4}}dx = \int_{0}^{\infty}\frac{3}{4}x^4e^{(-x^{3/4}+x)}e^{-x}dx$$

Considering the generalized Gauss-Laguerre quadrature:

$$\int_{0}^{\infty} x^{\alpha}f(x)e^{-x}dx$$ $$\begin{align}\alpha &= 4, & f(x) = \frac{3}{4}e^{(-x^{3/4}+x)}\end{align}$$

Results:

$\Gamma(\frac{20}{3})$ = 389.034926246

Gauss Laguerre (20 points) = 389.03475968

Gauss Laguerre (50 points) = 389.034926232