Asymptotic behavior of the zeros of the digamma function

Question

The gamma function has just one extremum on each interval $(k,k+1)$, where $k$ is a negative integer. These extrema occur at the zeros of the derivative of the gamma function. Let $z_n$ denote the $n$-th greatest zero, or the zero found on the interval $(-n, -n+1)$.

As $n$ grows, $z_n$ nears $-n$. In other words, $z_n+n=\{z_n\}=z_n-\lfloor z_n\rfloor$ nears $0$. I have numerically found $\{z_n\}^{-1}$ to be asymptotically equivalent to $\log(n)$:

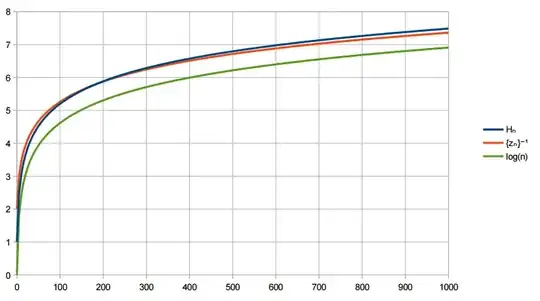
Here's the kicker, though. It seems that $\lim\limits_{n\to\infty}\left(\{z_n\}^{-1}-\log(n)\right)\approx 1-\gamma$.

I appear to be reaching the limits of double precision. At $n=1754$, I start getting (presumably) wildly inaccurate values for $z_n$. If my approximations can be trusted before this point, however, then $\{z_n\}^{-1}-\log(n)+\gamma$ decreases and reaches about $1$ at $n=1713$, but continues decreasing below $1$. If this is truly the case, then the claim in the previous paragraph is not a strict equality.

Does anyone know of a proof of $\{z_n\}^{-1}\sim\log(n)$ or if $\lim\limits_{n\to\infty}\left(\{z_n\}^{-1}-\log(n)\right)= 1-\gamma$ is true? I welcome any analytical or numerical evidence hinting at the confirmation or negation of either of these two statements.

I myself know next to nothing about the gamma function or its relatives, but I noticed the zeros drifting left on their intervals and decided to investigate.

Answer 1

I agree.

I get $\frac1{z_n} \approx \ln n$ and $n(\frac1{ z_n}-\ln n) \approx \frac12 $.

Here is my analysis.

There are two main ideas:

First, use the reflection formula for the Gamma function to move the analysis from large negative to large positive arguments.

Second, use the first two terms of the asymptotic formula for the digamma function.

The rest is in the details and here they are:

Since $\Gamma(z)\Gamma(-z) =-\frac{\pi}{z\sin(\pi z)} $, $\Gamma(-z) =-\frac{\pi}{z\Gamma(z)\sin(\pi z)} =-\frac{\pi}{\Gamma(z+1)\sin(\pi z)} $ so

$\begin{array}\\ \Gamma'(-z) &=-\left(\frac{\pi}{\Gamma(z)\sin(\pi z)}\right)'\\ &=\frac{\pi(\Gamma(z)\sin(\pi z))'}{(\Gamma(z)\sin(\pi z))^2}\\ &=\pi\frac{\Gamma'(z)\sin(\pi z)+\Gamma(z)\pi\cos(\pi z)}{(\Gamma(z)\sin(\pi z))^2}\\ \end{array} $

Therefore, $\Gamma'(-z) = 0$ when $\Gamma'(z)\sin(\pi z)+\Gamma(z)\pi\cos(\pi z) =0 $ or $\frac{\Gamma'(z)}{\Gamma(z)} =-\frac{\pi\cos(\pi z)}{\sin(\pi z)} =-\frac{\pi}{\tan(\pi z)} $.

Let $z = n+x$. My goal is to get $x$ as a function of $n$ such that $\Gamma'(z) = 0 $.

This means that we want $\frac{\Gamma'(n+x)}{\Gamma(n+x)} =-\frac{\pi}{\tan(\pi (n+x))} =-\frac{\pi}{\tan(\pi x)} $.

The asymptotic series for $\psi(z) =\frac{\Gamma'(z)}{\Gamma(z)}$ is (see http://mathworld.wolfram.com/DigammaFunction.html) $\psi(z+1) \approx \ln(z)+\frac1{2z} $.

Therefore, $\psi(n-1+x) \approx \ln(n+x)+\frac1{2(n+x)} $, so we want $\ln(n+x)+\frac1{2(n+x)} \approx -\frac{\pi}{\tan(\pi x)} $.

Since we want the fraction on the right to be about $\ln(n+x)$ which is not small, then $x$ must be small, so that $\tan(\pi x) \approx \pi x $. Substituting this, we want $\ln(n+x)+\frac1{2(n+x)} \approx \frac1{ x} $.

Since $\ln(n+x) =\ln n +\ln(1+\frac{x}{n}) \approx \ln n + \frac{x}{n} $, this becomes $\ln n + \frac{x}{n}+\frac1{2(n+x)} \approx \frac1{ x} $ or, eliminating the $O(\frac1{n})$ terms, $\ln n \approx \frac1{ x} +O(\frac1{n}) $ or $x \approx \frac1{ \ln n} +O(\frac1{n}) $.

Since $x \approx \frac1{ \ln n} $, we get $\frac1{ x} \approx\ln n + \frac1{n \ln n}+\frac1{2(n+\ln n)} \approx\ln n +\frac1{2n} + o(\frac1{n}) $ or $\frac1{ x}-\ln n \approx \frac1{2n}+ o(\frac1{n}) $ or $n(\frac1{ x}-\ln n) \approx \frac12 + o(1) $.

Note added later:

The reference supplied by Claude Leibovici has the result $z_k ≈ −k +\frac1{\pi} \arctan\left(\frac{\pi}{\ln k -\frac1{2k}+O(\frac1{k^2})}\right) $ which, I believe, agrees with mine.