6

In a commutative ring $R$ if $I,J,K$ are ideals, is $(I+J)\cap (I+K)=I+J\cap K$. I think this is true but cannot find it referenced anywhere. Working modulo $I$, both sides are just $J\cap K$ and since all ideals contain $I$, we can lift this relation to $R$? Am I thinking straight here? I am also a bit apprehensive since I cannot seem to make an element wise argument for the result.

I still cannot find any counterexamples. If anyone can suggest one it would be of great help. I am also unable to see the flaw in the above argument.

Wayne S
  • 111
  • @MartinBrandenburg: I did check both $\mathbb{Z}$ and $k[x]$. Maybe I just chose the "wrong" examples. – Wayne S Mar 13 '12 at 22:12

2 Answers2

11

Here's a counterexample in $\mathbb{Z}[x]$.

Let $I=(2)$, $J=(x-1)$, $K=(x+1)$. Then $J\cap K = (x^2-1)$. So $I+(J\cap K) = (2,x^2-1)$.

On the other hand, $I+J = (2,x-1) = (2,x+1) = I+K$, so $(I+J)\cap(I+K) = (2,x+1)$.

However, $(2,x+1)\neq (2,x^2-1)$, since $x+1\notin (2,x^2-1)$.

Arturo Magidin
  • 398,050
  • Thank you for the right counterexample. I wasted a lot of time working with $\mathbb{Z}$ after the first comment. Would this work under stronger conditions on the ring - say local or domain? – Wayne S Mar 14 '12 at 03:44
  • 2
    @Wayne: I think Martin misread $I+J\cap K$ as $(I+J)\cap K$ instead of $I+(J\cap K)$. The expression is ambiguous. The example I give is a domain (in fact, a UFD), so certainly "domain" is not enough. PID should work, using the same argument as for $\mathbb{Z}$. I don't think it would necessarily work under "local", but I am not sure. – Arturo Magidin Mar 14 '12 at 03:47
  • Nice answer, Arturo. (Btw, you have an extraneous math delimiter that the edit system won't let me fix for you.) – William DeMeo Mar 14 '12 at 03:52
  • @William: Got it; thank you. – Arturo Magidin Mar 14 '12 at 03:53
  • @Arturo: Is this counterexample also ok for $(I+J)\cap K \neq (I\cap K)+(J\cap K)$? I don't know how to compute $I\cap K$ and $J\cap K$ in terms of generators. – Leo Mar 16 '13 at 17:18
5

The property you are asking about is called the distributive law for lattices.

It's true that the lattice of ideals of a ring is modular, but it need not be distributive. Here is an easy counterexample, shown to me by Ralph Freese:

Let

$$R = \left\{ \left(\begin{array}{cc} x & y\\ 0 & z \end{array} \right) : x, y, z \in \{0, 1\} \right\}$$

This forms a ring with the usual matrix addition and multiplication.

Let $T$ be the ideal generated by $\left(\begin{array}{cc} 0 & 1\\ 0 & 0 \end{array} \right)$ in $R$. That is, $$T = \left\{\left(\begin{array}{cc} 0 & 0\\ 0 & 0 \end{array} \right), \left(\begin{array}{cc} 0 & 1\\ 0 & 0 \end{array} \right)\right\}.$$

Now consider the direct product $R\times R$. This is a ring with ideals $0\times T$, $T \times 0$, and $T\times T$ (among others). But there is also the "diagonal" ideal below $T\times T$, which is generated by $\left(\begin{array}{cc} 0 & 1\\ 0 & 0 \end{array} \right) \times \left(\begin{array}{cc} 0 & 1\\ 0 & 0 \end{array} \right)$.

So, the interval below $T\times T$ in the lattice of ideals of $R\times R$ is the modular (nondistributive) lattice which we call $M_3$.

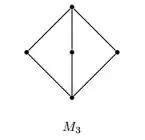
enter image description here

In your notation, you can take $I=T\times 0$, $J = 0\times T$, and $K$ equal to the diagonal ideal, and you will find that the distributive law fails:

$$(I+J)\cap(I+K) = T\times T \neq T\times 0 = I+(J\cap K).$$

William DeMeo
  • 3,636