I'm struggling to get to grips with the Triangle Inequalities. The problem is I don't really understand what it means. This is what my lecturer has written in the notes: $$ |a+b|≤|a|+|b|. $$ First of all, I don't understand why it's less than or equal to.
If I plug in numbers, for example $a=2$ and $b=5$, I struggle to see how $|2+5|≤|2|+|5|$.
If someone could explain this to me I would be very grateful.
OK. I will try to explain why $$ |a+b|\leq |a| + |b| $$ is true in a somewhat intuitive/pictorial way.
First off, do you know what $|x|$ means for some number $x$? You probably know that $|x|$ means the absolute value of $x$, but what does that even mean? The absolute value of a number $x$ may be thought of as its "absolute" distance from zero on the real number line. For example, how far away is $3$ from $0$? This is clearly $3$ units away. What about $-4$? Well, this is just $4$ units away from $0$ but in a different direction (remember, the only thing that matters is absolute distance and distances are always positive). Thus, we get the following definition for the absolute value of a number $x$: $$ |x|= \begin{cases} x &\text{if} & x\geq 0,\\ -x &\text{if} & x<0. \end{cases} $$ This guarantees us that the distance from $x$ to $0$ will always be positive, regardless of the value of $x$.
Phew. Okay. Now consider what $|a+b|\leq|a|+|b|$ means. What if $a$ is positive and $b$ is negative? What number will be larger: $|a+b|$ or $|a|+|b|$? Can you see how this might confirm the truth of the triangle inequality?
If you need more explanation or want a general proof (although I think a general proof may confuse you more than help you at the moment), then let me know and I'll add it.
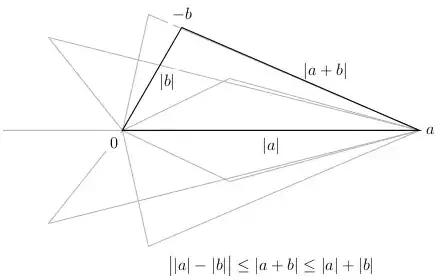
Suppose you supply two arbitrary real numbers $a$ and $b$. Let's construct a "triangle" (on the number line) whose vertices are $0$, $a$, and $-b$. (We're free to choose vertices as we like; pick $-b$ instead of $b$ for reasons to be explained in a moment.)
Since the distance between real number $x$ and $y$ is $|x - y|$, the sides of our "triangle" have lengths $$ |a - 0| = |a|,\qquad |-b - 0| = |-b| = |b|,\qquad |a - (-b)| = |a + b|. $$ (Now you know why we picked $-b$: To get $a + b$ inside the absolute value.:)
Two sides of our triangle have length $|a|$ and $|b|$. It's reasonable to ask: Based on this information alone, how long can the third side be?
It should be fairly clear geometrically that:
The third side cannot exceed $|a| + |b|$, the sum of the lengths of the known sides. In symbols, $$ |a + b| \leq |a| + |b|. $$ This is the triangle inequality.
The third side cannot be shorter than the distance between the real numbers $|a|$ and $|b|$. In symbols $$ |a + b| \geq \bigl||a| - |b|\bigr|. $$ This is the reverse triangle inequality.
In your particular example, if two sides of a triangle have length $2$ and $5$, then the third side cannot be shorter than $|2 - 5| = |-3| = 3$, and cannot be longer than $|2 + 5| = |7| = 7$. (On the number line, the sides of a "triangle" are parallel, so the third side is actually equal either to $3$ or to $7$. However, similar-looking inequalities hold for distance in the plane, or in space, or in higher-dimensional spaces. In these spaces, the sides of a triangle need not be parallel. In the plane, the third side of your triangle could have any length between $3$ and $7$.)
One nice proof of the triangle inequalities (for real numbers) is to show that if $x$ and $c$ are real numbers, then $|x| \leq c$ if and only if $-c \leq x \leq c$. (That is, an upper bound on the absolute value of $x$ can be "traded" for a symmetric pair of upper and lower bounds on $x$.)
Clearly, \begin{align*} -|a| &\leq a \leq |a| &&\text{for all real $a$,} \\ -|b| &\leq b \leq |b| &&\text{for all real $b$.} \\ \text{ Adding,}\quad -\bigl(|a| + |b|\bigr) &\leq a + b \leq |a| + |b|. && \end{align*} The third line has the form $-c \leq x \leq c$ for $x = a + b$ and $c = |a| + |b|$, and so can be "traded" for $|x| \leq c$, namely, for $$ |a + b| \leq |a| + |b|. $$ Note, in addition, that $$ |a - b| = |a + (-b)| \leq |a| + |-b| = |a| + |b|. $$
To prove the reverse triangle inequality, we apply the preceding reasoning to the equations \begin{align*} b &= (a + b) - a & \text{obtaining}\quad |b| &\leq |a + b| + |a|, \\ a &= (a + b) - b & \text{obtaining}\quad |a| &\leq |a + b| + |b|. \end{align*} Rearranging the inequalities on the right, we have $$ -|a + b| \leq |a| - |b| \leq |a + b|. $$ This chain of inequalities is also of the form $-c \leq x \leq c$, this time with $x = |a| - |b|$ and $c = |a + b|$, and so can be "traded" for $$ \bigl||a| - |b|\bigr| \leq |a + b|. $$
$a\le b$ means $a$ is less than or equal to $b$, so we have $3\le 3$ and $3\le 4$ for example, since $3$ is equal to $3$ and $3$ is less than $4$.
For example, $|2+5|=7=|2|+|5|$, so $|2+5|\le |2|+|5|$. And $|-1+5|=4<6=|-1|+|5|$, so $|-1+5|\le |-1|+|5|$.
I guess you are talking about the triangle equality for real numbers, and there is a hint:
When $ab\ge0$, show that $|a+b|=|a|+|b|$.
When $a<0<b$, show that $|a+b|<|b|<|a|+|b|$.
If you want to convince yourself that the statement is true, then you should break the statement part into cases: both $a$ and $b$ are positive, both $a$ and $b$ are negative, one is positive and the other is negative, etc.
If you want to know why it is called the triangle inequality, pick any $x$. Let $y = x - a$ and $z = y - b$. Then we have that $a = x - y$ and $b = y - z$. Thus, the inequality becomes: $$ |x - z| \le |x - y| + |y - z| $$
Now think of $x$, $y$, and $z$ as vertices of a triangle, and the absolute value as a distance function. Then the meaning is clear: the distance between $x$ and $z$ is shorter than the distance between $x$ and $z$ through the intermediate point $y$.
It's all about signed values.
When $a$ and $b$ have the same sign, you always get the strict equality. When the sign differs, you get the inequality.
The given inequation summarizes these two situations.
I think this is just triangular inequality in 1 dimension.
To proof it you square both side
There is a proof here already
$$(a+b)^2= a^2+b^2+2a\cdot b \leq a^2+b^2+2\left| a \right| \left| b \right| $$ $$(a+b)^2 \leq \left(\left| a \right| + \left| b \right|\right)^2$$
And the triangular inequality follows.
What you need to watch is what is $a\cdot b$ That is a real number defined by a binary operation of 2 products. Basically one theorem of the dot product is that the dot product will never exceed the size multiple of the vectors. I got to find the proof here.
So basically
$a\cdot b \leq \left| a \right| \left| b \right|$
The value is the same only if the vectors are in the exact same direction.
Now extend that to one dimension and your vectors only have 2 directions. They can both point toward positive or negative real numbers.
If the direction the same, the inequality becomes equality. If the direction is not, then the inequality hold.
$|x|$ means the absolute value of $x$. This means that if the value of $x<0$, then $|x|=-x$ otherwise $|x|=x$. In simple words, $|x|$ is formed by removing the minus sign from $x$, if any. So $|4|=4$ and $|-3|=3$
The equation states an obvious fact: $$|a+b|\leq|a|+|b|$$
If $a$ and $b$ are both positive, we have $|a+b|=|a|+|b|$, else we have $|a+b|<|a|+|b|$
Try putting these values, and you should be able to figuring it out: $(2,5)$, $(2,-5)$, $(-2,-5)$
What this has to do with a triangle is unclear to me, though.
