How can I know the function $$f(x,y)=\frac{y^2}{xy+1}$$ with $x>0$,$y>0$ is convex or not?
Asked
Active
Viewed 7.0k times
26
-
7Have you looked at the Hessian matrix? If it is positive semidefinite, $f$ is convex. – Michael Greinecker Mar 12 '12 at 20:37
-
I checked the Hessian matrix, but unfortunately it is indefinite. – Xiangyu Meng Mar 12 '12 at 20:51
-
8So the two eigenvalues of the Hessian have opposite signs, meaning one eigenvalue is negative. The function will be concave in the direction of the corresponding eigenspace. – Harald Hanche-Olsen Mar 12 '12 at 21:18
-
Thanks for your answer. I think it is a good suggestion. – Xiangyu Meng Mar 12 '12 at 22:13
3 Answers
22
Consider $y=x$ then we have $\displaystyle g(x)=\frac{x^2}{x^2+1}=1-\frac 1{x^2+1}$
The second derivative of this is $g''(x)=\frac{2-6x^2}{(1+x^2)^3}$ and will change sign around $x=\frac 1{\sqrt{3}}$ so that $g$ is convex in $(0,\frac 1{\sqrt{3}})$ and concave in $(\frac 1{\sqrt{3}},\infty)$.
Your function is clearly not convex nor concave on $(\mathbb{R^{+*}})^2$ but you could search more restricted sets if needed...
Here is a picture (from below) of your function (convex near $y=0$ and concave when $y$ becomes larger at least in the x=y direction, in the x=-y direction it looks convex...) :
Raymond Manzoni
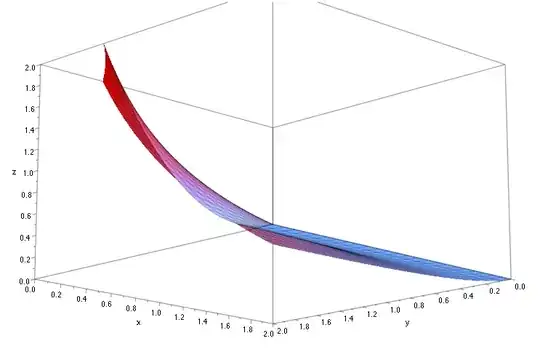
- 43,021
- 5
- 86
- 140
-
-
Simplify the problem to disprove convexity (it is a trick and proving complexity may require something like a Hessian for derivable functions). – Raymond Manzoni Aug 03 '20 at 14:17
-
yeah but you already know the answer about the convexity in advance right. Is there anyway to do this in an objective manner ? – Tuong Nguyen Minh Aug 05 '20 at 03:56
-
In fact I didn't know it was convex or not and set $y=x$ to get some intuition. The Hessian way proposed in the comments and by robjohn is the way to go for two variables or more for a differentiable real function. – Raymond Manzoni Aug 05 '20 at 08:22
14
The Hessian of $\frac{y^2}{1+xy}$ is $$ H = \frac1{(1+xy)^3}\begin{bmatrix} 2y^4&-y^2(3+xy)\\[12pt] -y^2(3+xy)&2 \end{bmatrix} $$ and $$ \begin{bmatrix} u&v \end{bmatrix} H \begin{bmatrix} u\\v \end{bmatrix} =\frac2{(1+xy)^3}(v-uy^2)^2-\frac1{(1+xy)^2}uvy^2 $$ Setting $\begin{bmatrix}u&v\end{bmatrix}=\begin{bmatrix}1&y^2\end{bmatrix}$ gives $$ \begin{bmatrix} 1&y^2 \end{bmatrix} H \begin{bmatrix} 1\\y^2 \end{bmatrix} =-\frac{y^4}{(1+xy)^2} $$ so $\frac{y^2}{1+xy}$ is not convex as long as $y\ne0$.
robjohn
- 345,667
-
What is the motivation for setting [$u$ $v$] = [$1$ $y^2$] ? – Tuong Nguyen Minh Aug 02 '20 at 13:31
-
We want to find a point which gives a negative value. $\frac2{(1+xy)^3}(v-uy^2)^2-\frac1{(1+xy)^2}uvy^2=-\frac{y^4}{(1+xy)^2}$ at $\begin{bmatrix}u&v\end{bmatrix}=\begin{bmatrix}1&y^2\end{bmatrix}$ – robjohn Aug 02 '20 at 14:18
9
The book "Convex Optimization" by Boyd, available free online here, describes methods to check.
The standard definition is if f(θx + (1 − θ)y) ≤ θf(x) + (1 − θ)f(y) for 0≤θ≤1 and the domain of x,y is also convex.
So if you could prove that for your function, you would know it's convex.
The Hessian being positive semi-definite, as mentioned in comments, would also show that the function is convex.
See page 67 of the book for more.
Jan Gorzny
- 902
-
Your answer is not useful. I think checking the eigenvalue of the Hessian matrix maybe a good approach. – Xiangyu Meng Mar 12 '12 at 22:13
-
4It is a very good book on the subject if you wish to go deeper than simple calculus. – Nick Alger Mar 12 '12 at 22:26
-
1Using the standard definition is almost always completely useless. The only time it is useful is if you have a function which is not continuous in its second derivative (or it doesn't exist) then you can rule out it is convex if you can numerically find a counter-example simply by randomly evaluating SEVERAL points. But this isn't generally practical or fun, nor can it ever prove a function IS convex, only that it isn't if you happen to find a counter-example. – Squirtle Jul 29 '13 at 23:47
-
2@Squirtle, it can absolutely prove a function is convex: if you show a function satisfies that condition, it is convex. As a basic example, let f(x)=5x and you will see that that condition is always an equality. Therefore f(x)=5x is convex everywhere. – Rasputin Jul 17 '17 at 19:53