1

I have a question on how the number of the first layer of the Graham's number ($g_1$) is computed.

From Wikipedia:

http://en.wikipedia.org/wiki/Graham%27s_number#Magnitude

$g_1 = 3\uparrow\uparrow\uparrow\uparrow3 $

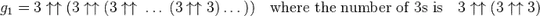
enter image description here

As I understand it, this means that the number of the first layer of the Graham's number $g_1$ is a tetration ($\uparrow\uparrow$) in the form:

$$g_1 = 3^{3^{\cdot^{\cdot^{\cdot^{\cdot^{3}}}}}} = \,{}^{n}3$$

Where $n$ is:

$3\uparrow\uparrow(3\uparrow\uparrow3) = \,{}^{7625597484987}3$

Thus, the height of the tower, is this what Wikipedia says?

If so, now, if:

$$3\uparrow\uparrow3 = \,{}^{3}3 = 3^{3^{3}}$$

$$3\uparrow\uparrow\uparrow3 = 3\uparrow\uparrow(3\uparrow\uparrow3)= \,{}^{3\uparrow\uparrow3}3 = \,{}^{7625597484987}3$$

Why g1 is (as in the posted link):

$$g_1 = 3\uparrow\uparrow\uparrow\uparrow3 = 3\uparrow\uparrow\uparrow(3\uparrow\uparrow\uparrow3)$$

And not:

$$g_1 = 3\uparrow\uparrow\uparrow\uparrow3 = 3\uparrow\uparrow(3\uparrow\uparrow\uparrow3)$$

??? Anyway, why:

$\,\,3\uparrow\uparrow\uparrow(3\uparrow\uparrow\uparrow3)\,\,\,\,\,$ is $\,\,\,\,\,3\uparrow\uparrow(3\uparrow\uparrow(3\uparrow\uparrow ... (3\uparrow\uparrow3)...))$

user3019105
  • 499
  • A discussion of this can also be found at http://www.mpmueller.net/reihenalgebra.pdf (However I don't know whether this is really helpful for you, since your notations seem to be very similar to that what I remember from an early version of the article) – Gottfried Helms Mar 15 '15 at 21:06
  • Thanks for the link! After rereading the example on Wikipedia I understood the principle: $3\uparrow\uparrow\uparrow\uparrow3$ refers to a recursive-recursive tetration repeated 3 times ($3\uparrow\uparrow\uparrow(3\uparrow\uparrow\uparrow3) = 3\uparrow\uparrow\uparrow(3\uparrow\uparrow(3\uparrow\uparrow3))$ which in turn means a recursive tetration repeated $3\uparrow\uparrow(3\uparrow\uparrow3)$ times, where $3\uparrow\uparrow(3\uparrow\uparrow3)$ is not the height of the tower, but the number of tetrations which overwrap one after each other, leading to an even bigger number. – user3019105 Mar 17 '15 at 08:24
  • Possibly of interest: Graham's Number : Why so big? – MJD Mar 30 '15 at 20:09

1 Answers1

2

The equality $3\uparrow\uparrow\uparrow\uparrow3=3\uparrow\uparrow(3\uparrow\uparrow3)$ is wrong there.

Hyperoperation (from tetration and so on) written in Knuth's notation satisfy the relation: $a\uparrow^nb=a\uparrow^{n-1}a\uparrow^{n-1}a\uparrow^{n-1}\dots \uparrow^{n-1}a$ where $n$ is the number of arrows, and $\uparrow^{n-1}$ is iterated b times.

So the first layer which is $3\uparrow\uparrow\uparrow\uparrow\uparrow2$ or (more usually) $3\uparrow\uparrow\uparrow\uparrow3$ is equal to:

$3\uparrow\uparrow\uparrow\uparrow3=3\uparrow\uparrow\uparrow3\uparrow\uparrow\uparrow3=3\uparrow\uparrow\uparrow(3\uparrow\uparrow3\uparrow\uparrow3)=3\uparrow\uparrow\uparrow(3\uparrow\uparrow7625597484987)$

So after you exponentiate 3 to itself 7625597484987 times you get how many times you have to tetrate 3 to itself, and that's only the first layer!

dan
  • 162
AlienRem
  • 4,011
  • Yeah, that's a really big thing, can't even imagine it with a number... – user3019105 Mar 31 '15 at 07:43
  • 1
    We can't imagine it, it has more digit than particles in the whole universe! If you try to compute that with your mind you'll probably collapse in a blackhole. (I don't remember where i read this). – AlienRem Mar 31 '15 at 09:30
  • And trying to compute the Ackermann's function of two Graham's number (xkcd -> http://xkcd.com/207/) as parameters will probably make the whole universe collapse in a blackhole. Not saying about what's behind of it, if anything. – user3019105 Mar 31 '15 at 13:21
  • Your 1st sentence states an inequality, which is true :). – dan Jan 01 '16 at 13:00