Why does squaring of the radius of a circle times pi give us the area?

Question

Why does squaring the radius of a circle times pi equal the area? (I.e., why does the area of circle representable as $\pi r^2$ ?)What is the relationship between the radius of a circle and the area?

Answer 1

I prefer the following illustration.

"CircleArea" by Jim.belk - Own work. Licensed under Public Domain via Wikimedia Commons.

Answer 2

Check this: Calculus proof for the area of a circle

And this: http://en.wikipedia.org/wiki/Area_of_a_disk#Onion_proof

Answer 3

Essentially, you need to square some linear measure of the circle to get to an area. The radius and the circumference are in any case related by a constant - $2\pi$ - and it happens that squaring the radius gives the simplest constant to obtain the area.

There is a pretty visual of how the area and radius are related here.

Answer 4

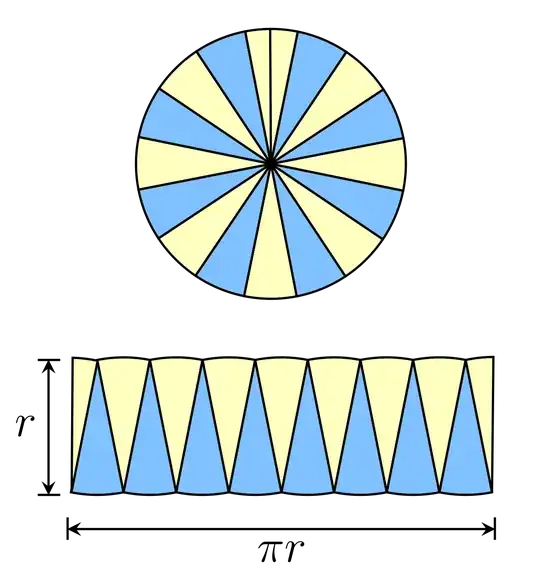
if you assume that $\pi$ is the ratio of the diameter of the circle to the circumference, then you can divide the circumference, say, into $1000$ points at equal distance. now join each of these segments to the center to make a small pie. arrange the pieces so that they make an almost rectangle of length $\pi \times \text {radius}$ and width the radius of the circle. the area of this rectangle is $\pi$ times the radius squared.