I have this part:
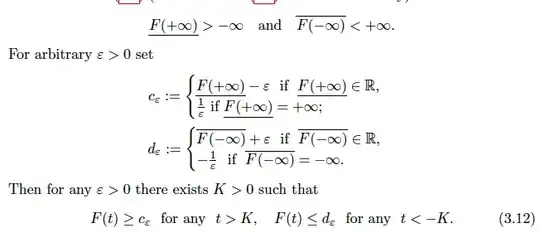
Where $$\underline{F(+\infty)}=\liminf_{x\rightarrow +\infty} F(x), \overline{F(-\infty)}=\limsup_{x\rightarrow-\infty} F(x)$$
My question is: How does property $(3.12)$ follow from the given information?
Thank you in advance.
I have this part:
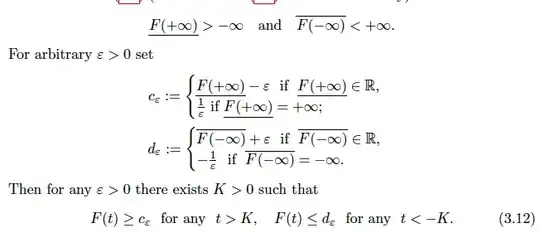
Where $$\underline{F(+\infty)}=\liminf_{x\rightarrow +\infty} F(x), \overline{F(-\infty)}=\limsup_{x\rightarrow-\infty} F(x)$$
My question is: How does property $(3.12)$ follow from the given information?
Thank you in advance.
Hint: If for some $\epsilon>0$ and for any $K>0$, $F(t)<c_\epsilon$ for some $t>K$, how could the $\liminf$ be larger than $c_\epsilon$?
More details:
Assume $\liminf_{x\rightarrow\infty} F(x)=\infty$ and there exists $\epsilon$ such that for any $K>0$, $F(t)<1/\epsilon=c_\epsilon$ for some $t>K$.
This means that no matter how far out you look towards positive infinity, there will always be an $x$ value such that $F(x)<1/\epsilon$, which is finite. Therefore, the limit infemum cannot possibly be infinite as there is always a larger $x$ value which gives a function output lower than $1/\epsilon$.
Similar arguments will work in the remaining 3 cases.
When you have trouble understanding the mathematics, especially complicated notation like this problem, it's a good idea to look at a more concrete example.
Let $F(x)=x$, so that $\liminf_{x\rightarrow+\infty} F(x)=+\infty$. Now fix $\epsilon$, say $\epsilon=1/10$. Therefore $c_\epsilon=2$. Now we can let $K$ be any number larger than $10$, thus for any $x>K$, $F(x)>c_\epsilon$.
Try to find the opposite of property 3.12 here. Can you find an $\epsilon$ such that $F(x)$ will always be smaller than $1/\epsilon$ if it is diverging to infinity?