This naive question came as the last problem in my homework. The author asked me to use linear relations of the discriminant like $\operatorname{disc}(ra_{1},a_{2},...,a_{n})=r^{2}\operatorname{disc}(a_{1},...,a_{n})$, $\operatorname{disc}(a_{1}+\beta,a_{2},...,a_{n})=\operatorname{disc}(a_{1},...,a_{n})$ for $\beta$ a linear combination of $a_{i}$. I could not see how to make use of the hint or how to solve the problem in an easier way than taking the norm and evaluate, which is impractical since $46\times 23$ terms are involved.
-
Do you mean irreducible as an element in $\mathbf Z[\omega]$? – Dylan Moreland Mar 08 '12 at 07:11
-
Remember that for a general number field $K$ with integers $\mathcal O$ and $\alpha \in \mathcal O$ we have $|N^K_{\mathbf Q}(\alpha)| = (\mathcal O : (\alpha))$. This last number is something you could get from relating the discriminants of $\mathcal O$ and $(\alpha)$. What's a good basis for the latter? – Dylan Moreland Mar 08 '12 at 07:12
-
1You may find something useful in the links in my answer to http://math.stackexchange.com/questions/85520/fermats-last-theorem-and-kummers-objection – Gerry Myerson Mar 08 '12 at 11:20
-
@DylanMoreland: I could prove it is irreducible in $A\cap \mathbb{Q}(\sqrt{-23})$, but I could not prove it is irreducible in $A\cap \mathbb{Q}(\omega)$. – Kerry Mar 08 '12 at 14:30
-
@DylanMoreland: I think it is a naive approach, but supoose $(2)\in (\alpha)$, and write $\alpha=\sum^{22}{i=0} a{i}\omega^{i}$. Then by your hint we have $|N(\alpha)|=(\mathbb{Z}[\omega]/\alpha)$. But this is not very clear - oh, do you mean using the integral basis of $O$ including $\alpha$? – Kerry Mar 08 '12 at 17:01
-
@ChangweiZhou It seemed like a way to use your hint. Now I'm not so sure. I'll try to think about it later. – Dylan Moreland Mar 08 '12 at 17:21
-
@DylanMoreland: I should ask my professor about this on class. – Kerry Mar 08 '12 at 17:59
-
@GerryMyerson: The links you gave in that page is only tangentially related to this problem. But the factorization you give is very surprising to me. – Kerry Mar 10 '12 at 06:10
-
@ChangweiZhou I don't think it's trivial to prove that $2$ is irreducible in the given number ring. – Dec 26 '12 at 01:04
2 Answers
We recall that a non-zero non-unit of a ring $S$ is said to be irreducible if it cannot be written as the product of two non-units. Set $S = \Bbb{Z}[w]$ now that is the ring of integers of the algebraic number field $\Bbb{Q}(w)$. $w = e^{2\pi i/23}$ here.
Now suppose that $2 = \alpha\beta$. We want to show that one of $\alpha$ or $\beta$ is a unit. Suppose that the both of them are not units. Then we have $2S = (\alpha\beta) = (\alpha)(\beta)$ with the ideals $(\alpha),(\beta)$ both properly contained in $\Bbb{Z}[w]$. Now by Proposition 10.3 (Neukirch) s, we know that the ideal $2\Bbb{Z}$ is unramified in $S$; in fact it is the product of $22/11 = 2$ prime ideals in $S$. I leave it to you to check that
$$2S = \left(2, \frac{1 + \sqrt{-23}}{2}\right)\left(2, \frac{1 - \sqrt{-23}}{2}\right).$$
By unique factorisation, we must have $(\alpha) = \left(2, \frac{1 + \sqrt{-23}}{2}\right) = Q$ say. However this contradicts $Q$ not being principal and so at least one of $\alpha$ or $\beta$ must be a unit in $\Bbb{Z}[w]$.
Proof that $Q$ is not principal, à la Marcus Problem 3.17:
Let $K = \Bbb{Q}(\sqrt{-23})$, $L = \Bbb{Q}(w)$. By my answer here we know that $K\subseteq L$. Set $R = \mathcal{O}_K$ and $S = \mathcal{O}_L$.
Part (a): Let $P$ be the prime ideal $(2, \theta)$ in $R$ that lies over $(2)$ in $\Bbb{Z}$ where $\theta = \frac{1 + \sqrt{-23}}{2}$. Now if $Q$ is a prime of $S$ that lies over $P$ then it also lies over $(2)$ in $\Bbb{Z}$. By Proposition 10.3 (Neukirch) we have $$e(Q|(2)) = \varphi(2^0) = \varphi(1) = 1$$ and $f(Q| (2)) = 11$ because $2^{11} = 1 + 23(89)$ and one easily sees that $11$ is the multiplicative order of $2 \pmod{23}$. Since the inertia degree is multiplicative in towers, we get that
$$f(Q|P) = \frac{f(Q|(2))}{f(P|(2))} = \frac{11}{{f(P|(2))}}.$$
Now since $-23 \equiv 1 \pmod{8}$ by knowledge of how primes split in quadratic extensions we know that $2R = (2,\theta)(2,\bar{\theta})$ where $\bar{\theta}$ is the other Galois conjugate of $\theta$ over $\Bbb{Q}$. It will now follow that $f(P|(2)) = 1$ and so we conclude that $f(Q|P) = 11/1 = 11$. For the last part of this problem, we know already that $S/PS$ is an $11$ - dimensional $R/P$ vector space. Since this is equal to $f(Q|P)$, we see that the map $f$ in the diagram
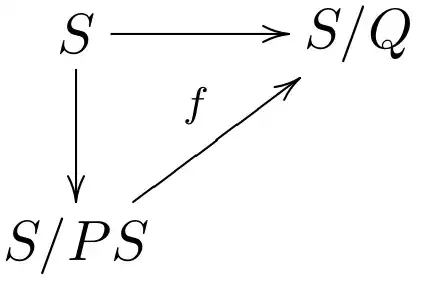
is a surjective map between two finite sets of the same size and hence is injective. It follows that $PS = Q$, i.e. that $(2,\theta) = Q$ in the ring $S = \Bbb{Z}[w]$.
(b): Now it is not hard to see that $P^3 = (\theta - 2)$. If $P$ is a principal ideal generated by some $\alpha \in R$ then since $||P||^3 = ||(\theta - 2)|| = 8$ and so we would have $N_{K/\Bbb{Q}}(\alpha)$ being either $2$ or $-2$. We now show that there is no element in $R$ of norm $2$ or $-2$. Consider a general element $x$ in $R$ which is of the form $x = a + b \theta$ for $a,b \in \Bbb{Z}$. Then $N_{K/\Bbb{Q}} (x) = (a + b\theta)(a + b\bar{\theta}) = a^2 + ab + 12b^2$. If this is equal to $2$ or $ -2$, by the quadratic formula there must exist an integer $b$ such that $b^2 - 4(12b^2 -2) \geq 0$ or $b^2 -4(12b^2 +2) \geq 0$ which is a contradiction. It follows that $P$ is not principal.
(c) - Final part of the proof to show that $Q$ is not principal: Let $G(S)$ and $G(R)$ denote the ideal class gorups of $R$ and $S$. Let $d_Q$ denote the order of the class of $Q$, let $d_P$ denote the order of the class of $P$. If $Q$ is a principal ideal then we would have $d_Q = 1$. By my answer here and by part (a) of this problem we would have $d_P|11$. However from (b) we have $P^3 = (\theta - 2)$ and taking ideal classes gives $[P]^3 = [(\theta - 2)]$ where the latter is the class of the identity. We conclude that the order of $[P]$ is exactly $3$ because $P$ is not principal. However we now get that $3|11$ which is a contradiction from which it follows that $Q$ cannot possibly be principal.
$$\hspace{6in} \square$$
"Number Fields" by Daniel A. Marcus has a guided exercise that proves your question - see chapter 3, exercise 17 (page 86):
- 6,245