What are some rigorous definitions for sine and cosine?

Question

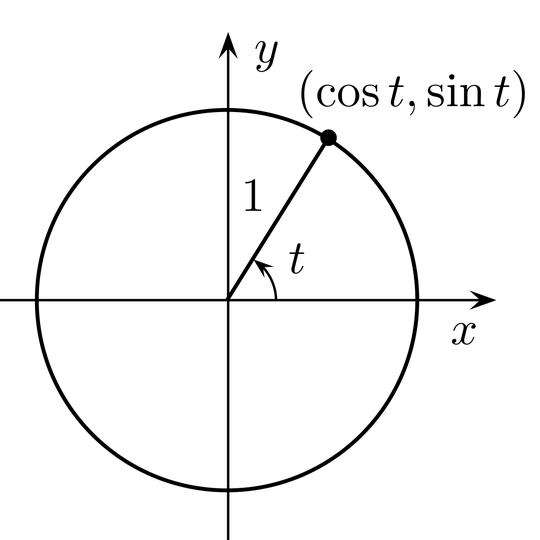
Here are some of my ideas:

1. Addition Formula: $\sin{x}$ and $\cos{x}$ are the unique functions satisfying:

• $\sin(x + y) = \sin x \cos y + \cos x \sin y $

• $\cos(x + y) = \cos x \cos y - \sin x \sin y$

• $\sin 0 = 0\quad$ and $\quad\displaystyle{\lim_{x \rightarrow 0} \frac{\sin x }{x} = 1}$

• $\cos 0 = 1\quad$ and $\quad\displaystyle{\lim_{x \rightarrow 0} \frac{1-\cos x}{x} = 0}$

2. Taylor Series:

• $\displaystyle{\sin x = \sum_{n = 0}^{\infty} \frac{(-1)^n}{(2n+1)!}\;x^{2n+1}}$

• $\displaystyle{\cos x = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n)!}\;x^{2n}}$

3. Differential Equations: $\sin(x)$ and $\cos(x)$ are the unique solutions to $y'' = -y$, where $\sin(0) = \cos^\prime(0) = 0$ and $\sin^\prime(0) = \cos(0) = 1$.

4. Inverse Formula: We have:

$$\begin{align} \arcsin x &= \phantom{\frac{\pi}{2} + } \int_0^x \frac{1}{\sqrt{1 - t^2}}\, dt \\[6pt] \arccos x &= \frac{\pi}{2} - \int_0^x \frac{1}{\sqrt{1 - t^2}}\, dt \end{align}$$

Then $\sin x$ is the inverse of $\arcsin x$, extended appropriately to the real line, and $\cos x$ is similar.

Question: Are there any others that you like? In particular, are there any good rigorous ones coming from the original geometric definition?

Answer 1

The book Principles of Mathematical Analysis (also called Baby Rudin) by Walter Rudin, Second edition, pages 167-169, briefly develops the theory of trigonometric functions. This is after developing the theory of series of complex numbers as well as the theory of exponential and logarithmic functions, so the additional analysis can be quite brief.

Rudin defines the complex exponential function $E(z)$ by

$$E(z)=\sum_{n=0}^{\infty} \frac{z^n}{n!}$$

then defines the functions cosine and sine (which he initially calls $C(x)$ and $S(x)$) of a real variable by

$$C(x)=\frac 12[E(ix)+E(-ix)], \quad S(x)=\frac 1{2i}[E(ix)-E(-ix)]$$

He then derives all the usual properties (both trigonometric and analytic) of sine and cosine in just two pages. All his proofs are simple and clear, except for one: showing that there are positive numbers $x$ such that $C(x)=0$. That can be proved simply in other ways, so the analytic exposition of trigonometry is rigorous, brief, and clear. Along the way he also shows the usual parameterization of the unit circle and shows the usual high-school definitions of sine and cosine.

Rudin's conclusion is,

It should be stressed that we derived the basic properties of the trigonometric functions from [the definitions of $E(x)$, $C(x)$, and $S(x)$], without any appeal to the geometric notion of angle.

(I replaced references to specific equations with their meaning in this quote.)

---

Regarding your question "In particular, are there any good rigorous ones coming from the original geometric definition?":

The "original geometric definition" is not rigorous unless you have a good definition of the length of a circular arc as well as a good axiom system for the real numbers or an equivalent. Euclid did not provide such a system, though he tried. The explanation I gave from Baby Rudin defines geometry and trigonometry from analysis. Developing a rigorous geometry that includes all the trigonometric ideas without starting from analysis is very difficult. Even Hilbert's axioms for geometry had its problems. I have never seen a good rigorous development of trigonometry from modern formal geometry, though it must exist somewhere.

Answer 2

My preferred definition is:

$\cos x$ and $\sin x$ are the real and imaginary parts of the exponential function $\exp(ix)$.

Since we have: $$ \begin{split} e^{ix}= \sum_{k=0}^\infty\dfrac{(ix)^k}{k!}&=1+ix+\dfrac{(ix)^2}{2!}+\dfrac{(ix)^3}{3!}+\cdots+\dfrac{(ix)^n}{n!}+\cdots\\ &=1-\dfrac{(x)^2}{2!}+\dfrac{(x)^4}{4!}-\dfrac{(x)^6}{6!}+ \cdots +i\left[ x-\dfrac{(x)^3}{3!}+\dfrac{(x)^5}{5!}+\cdots \right]\\ &= \sum_{k=0}^\infty\dfrac{(-1)^k\,x^{2k}}{(2k)!}+i \sum_{k=0}^\infty\dfrac{(-1)^k\,x^{2k+1}}{(2k+1)!}\end{split} $$ we find the usual series definitions.

Answer 3

One definition that I think has a very clear geometric meaning is this: On the unit circle in the $xy$-plane, draw a line segment from the origin to a point on the circle. Call the angle that the line segment makes with the $x$-axis $t$ as shown in the picture. We define the $x$-component of the endpoint of the line segment as $\cos(t)$ and the $y$-component as $\sin(t)$.

The trig class "opposite, ajacent, hypotenuse" definition follows from this one. It is also not too difficult to derive inverse function integral definition from this. The addition formula definition is a bit more work to obtain, but there are geometric proofs of all of the facts listed.

Answer 4

Here's one way:

1. Define some basic operations like integration and analytical continuation.
2. Set $\ln x=\int_1^x \frac{dt}{t}.$
3. Set $\exp=\ln^{-1}$ (the inverse function).
4. Extend $\exp$ from $\mathbb R$ to $\mathbb C$ by analytical continuation.
5. Finally set $$ \sin(z)=\frac{\exp(iz)-\exp(-iz)}{2i},\quad \cos(z)=\frac{\exp(iz)+\exp(iz)}{2}. $$

Answer 5

Here's a way to formalize the geometric intuition. We can define $\sin,\cos$ as the projections of the helix $\text{cis}(x)=:(\cos(x),\sin(x))$, where $\text{cis}:\mathbb{R}\to\mathbb{R}^2$ is the unique $C^1$ rectified path in the unit circle which starts from $(1,0)$ and travels counterclockwise.

• $\text{cis}\in C^1$
• $||\frac{d}{dx}\text{cis}(x)||=1$
• $||\text{cis}(x)||=1$
• $\text{cis}(0)=(1,0)$
• $\frac{d}{dx}\text{cis}(x=0)\neq (0,-1)$

Also, you could modify the addition formula characterization to avoid calculus almost entirely.

• $\sin\cos\in C^0$
• $\sin(x+y) = \sin(x)\cos(y) + \cos(x)\sin(y)$
• $\cos(x+y) = \cos(x)\cos(y) - \sin(x)\sin(y)$
• $\cos(x)^2+\sin(x)^2=1$
• $\forall(x\in(0,\pi]), \sin(x)\leq 0 \iff x=\pi$

The first three conditions can show that the function $\text{cis}(x):=(\cos(x),\sin(x))$ is either zero or a logarithmic spiral with $\text{cis}(0)=(1,0)$. The fourth condition narrows it down to a helix, and the final condition decides the orientation, with $\pi$ defining the wavelength. You still need to define $\pi$ though, which requires calculus unfortunately. On the plus side, this highlights how $\pi$ is only special in how angles correspond to arclengths.

For example, if you replace $\pi$ in the last condition with some positive constant $\lambda$, this would define the trig functions in terms of different units for angles (such as degrees, if $\lambda=180$), and wouldn't require any calculus beyond basic continuity. You could omit the continuity condition if you only need to define $\sin,\cos$ for rational multiples of the wavelength $\lambda$.