Urgent help requested!! Anything I can do to get an answer faster, in terms of my question??
The question, diagram, and my work are attached. Any help or suggestions or hints are extremely welcome and appreciated.

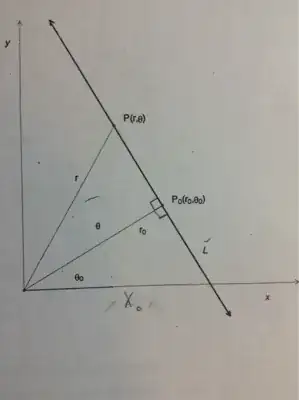 My apologies for the tags. I couldn't find one that accurately described the content in this question. Also apologies for the bad title. Doing this on a mobile device and I had too many characters and then it made me wait for 30-60 seconds.
My apologies for the tags. I couldn't find one that accurately described the content in this question. Also apologies for the bad title. Doing this on a mobile device and I had too many characters and then it made me wait for 30-60 seconds.
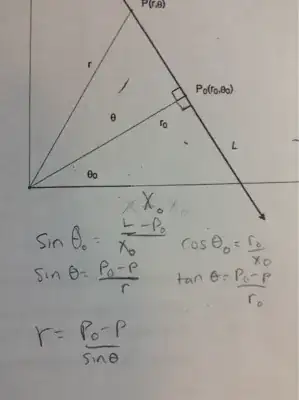
More of my ideas.