We know that
$$\dbinom{n}r = \dfrac{n!}{(n-r)!r!}$$
An intuitive explanation of the formula is that, if I partition the total number of permutations of objects by $r!$, and choose one member of each partition, then no similarly ordered pattern will be registered more than once.
Is there a more intuitive explanation than this?
Think of it this way. Suppose that I have balls numbered $1$ through $n$, I want to pick $r$ of them, and I do it one ball at a time. There are $n$ different ways in which I could choose the first ball. Once it’s been chosen, there are only $n-1$ balls left, so there are $n-1$ different ways in which I could pick the second ball. Thus, there are $n(n-1)$ different ways in which I could pick the first two balls. If I continue in this fashion, after I’ve picked $r-1$ balls, there will be $n-(r-1)=n-r+1$ balls left, so I’ll be able to pick the $r$-th ball in $n-r+1$ different ways. Thus, the sequence of $r$ balls can be chosen in
$$n(n-1)(n-2)\ldots(n-r+1)=\frac{n!}{(n-r)!}\tag{1}$$
different ways. The $(n-r)!$ in the denominator merely serves to cancel out the unwanted factors in $n!$.
However, $(1)$ is the number of different sequences of $r$ balls that we could choose: if $B$ is a set of $r$ balls, $(1)$ counts every possible permutation of the balls in $B$ separately. For example, if $B=\{b_1,b_2,b_3\}$, expression $(1)$ counts $B$ six times, once for each of the $3!=6$ possible sequences in which we could have chosen $B$: $\langle b_1,b_2,b_3\rangle,\langle b_1,b_3,b_2\rangle,\langle b_2,b_1,b_3\rangle,\langle b_2,b_3,b_1\rangle,\langle b_3,b_1,b_2\rangle$, and $\langle b_3,b_2,b_1\rangle$.
The same reasoning that I used to arrive at $(1)$ shows that there are $r!$ different ways to arrange a set of $r$ balls in order, so each $r$-element set of balls has been counted $r!$ times in $(1)$. Thus, to get the actual number of $r$-element subsets of our set of $n$ balls, we must divide $(1)$ by $r!$, getting
$$\binom{n}r=\frac{n!}{(n-r)!r!}\;$$
From the standpoint of seeing why this works, it’s better to think of it as
$$\frac{n(n-1)(n-2)\ldots(n-r+1)}{r!}=\frac{\prod_{i=0}^{r-1}(n-i)}{r!}\;;$$
that actually reflects the reasoning involved.
Here's a visualisation (following the reasoning which Brian outlined above) for those more visually inclined to see what's going on: https://charleslow.github.io/binomial_coefficient/
Let's say you have $n$ letters and you want the number of permutations of length $r$ from your alphabet. You have $n$ choices for the first letter, $n-1$ choices for the second letter, and so on for all $r$ of your letters. Thus the number of permutations is $\frac{n!}{(n-r)!}$.
Combinations are permutations where order doesn't matter. Instead of caring about which letter is first, which is second, etc., you only care about which letters you have. Your $r$ letters you've chosen can be ordered in $r!$ ways, so to get rid of the ordering, divide by $r!$.
These will certainly suffice, and other Khan Academy videos (Link 3) will be of further help.
Imagine writing down a list of all the possible combinations where you select $r$ items out of $n$. For each combination, there are $r!$ ways of ordering it. Therefore, each combination corresponds to $r!$ permutations, giving us the formula $P(n,r)=r!\times C(n,r)$. Since $P(n,r)=n!/(n-r)!$, the desired result immediately follows.
Here is a rather long, but, hopefully, intuitive, understanding of the formula for the binomial coefficients and Pascal's triangle. This post will use two expressions $(x+y)^n$ and $[f\cdot g]^{(n)}$, where the second expression refers to the $n$th derivative of two multiplied functions, to help with this intuition. At first glance, these expressions appear unrelated, but, when abstracted sufficiently, we will see that they are conceptually identical. Specifically, we will explore why $(x+y)^n=\displaystyle\sum_{k=0}^n \binom{n}{k}x^ky^{n-k}$ and why $[f \cdot g]^{(n)}=\displaystyle \sum_{k=0}^n \binom{n}{k}f^{(k)}g^{(n-k)}$...you should immediately see the similarity between the formulas, both involving the binomial coefficients.
To begin with, we will examine a picture where we have a starting position at some point $O$ and, every round, we can choose to either go $L$eft some positive distance ($\color{blue}{\text{blue}}$ arrow) or $R$ight some positive distance ($\color{red}{\text{red}}$ arrow). Every round, we will keep a running count of all moves made up to that point in time, where the recency of the move is determined by its left-to-right text location...for example, $LRL$ means that the first round movement was left, the second round movement was right, and the third round movement was left.
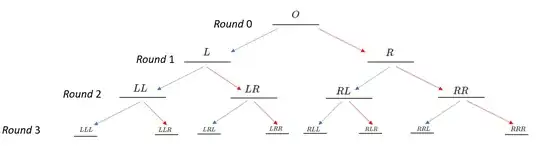
Now, suppose the distance traversed when choosing the '$L$eft path' is the same distance traversed when choosing the '$R$ight path.' Referencing the terms in Round 2, you should see that $LR$ places you at the exact same location as $RL$. Similarly, for Round 3, $LLR$, $LRL$, and $RLL$ would all bring us to the same location, as would $RRL$, $RLR$, and $LRR$. If we then ask, for a given round, how many ways are there to arrive at one of the possible locations, you should see how Pascal's triangle emerges.
Compare the above photo to the below two, where the $L$eft and $R$ight paths for the $(x+y)^n$ depiction correspond to multiplication by $x$ and multiplication by $y$, respectively; the $L$eft and $R$ight paths for the $[f\cdot g]^{(n)}$ depiction correspond to differentiating the $g^{(k)}$ term while treating the $f^{(j)}$ term constant and differentiating the $f^{(k)}$ term while treating the $g^{(j)}$ term constant, respectively.
$(x+y)^n$ Depiction:
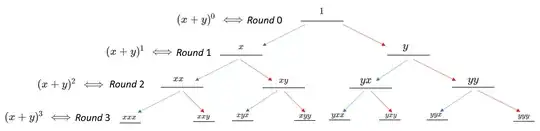
In the this depiction, you will notice that the terms found in each round, when summed, produce the terms found in $(x+y)^{\text{Round #}}$. Why is this so? Well, looking at $(x+y)^2$, note that by the distributive property of multiplication, this is just the summation of the terms $x\cdot (x+y)$ and $y\cdot(x+y)$, which we can rewrite as $x\cdot x$, $x \cdot y$, $y \cdot x$, and $y \cdot y$. But this precisely coincides with the terms that are generated through the blue / red arrows from Round 1 to Round 2. Similarly, $(x+y)^3=(x+y)\cdot(x+y)^2=x\cdot(x+y)^2+y\cdot(x+y)^2$, which once again mimics the blue / red arrow structure because $(x+y)^2$ encodes all elements from Round 2...and all said elements are subject to a blue arrow path (multiplication by $x$) and a red arrow path (multiplication by $y$). Moreover, much like in our traveling positive distances example where we assumed that the $L$eft distance traveled was equal to the $R$ight distance traveled, because multiplication is commutative, we see that $xy=yx$. Similarly, for Round 3, we have that $xyy=yyx=yxy$ and $xxy=xyx=yxx$. This description shows that the computation of $(x+y)^n$ exhibits the same structure as Picture 1's $L$eft / $R$ight structure.
$[f\cdot g]^{(n)}$ depiction
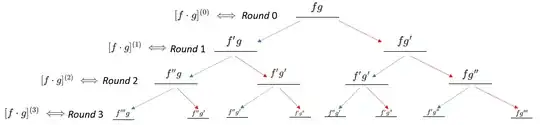
In the this depiction, you will notice that the terms found in each round, when summed, produce the terms found in $[f\cdot g]^{(\text{Round #})}$ As with the $(x+y)^n$ computation, there are properties of the derivative that make the computation of $[f \cdot g]^{(n)}$ structurally identical to the $L$eft / $R$ight traveling depiction. Firstly, for any two functions multiplied together, we know by the product rule that $[\phi \cdot \omega ]'=\phi'\omega +\phi \omega'$. In the $[f \cdot g]^{(n)}$ depiction, this is precisely what the blue arrow / red arrows do! Moreover, because the derivative is a linear operator, we know that $[\phi+\omega]'=\phi'+\omega'$. This feature combined with the previous feature ensure that differentiating the sum of all terms found in a given round is equivalent to taking the derivative of each individual term in that row.
Finally, because of how we described the actions of the red and blue arrows, it should be obvious which terms in a given round are equal to one another. This description shows that the computation of $[f\cdot g]^{(n)}$ exhibits the same structure as Picture 1's $L$eft / $R$ight structure.
With these concepts detailed, you are hopefully willing to believe that the computation of $[f\cdot g]^{(n)}$, or the computation of $(x+y)^n$, is equivalent to the original $L$eft / $R$ight traveling picture we first drew. With that established, we can now just refer to the "$L$eft / $R$ight traveling equal positive distances" structure to derive the binomial coefficients.
Deriving the binomial coefficients:
Firstly, for a given round, we can readily see that the total number of paths traversed is equivalent to $2^{\text{Round #}}$ because each path from the predecessor round bifurcates into two new paths. If I were to ask you to list an example of a traversed path from round $0$ to round $5$, the following is a valid response: $L\rightarrow L\rightarrow R \rightarrow R \rightarrow L$. If we view each round as establishing a temporal relationship (i.e. round 1 takes place before round 2, round 2 takes place before round 3, etc) then we could ask the following: "How many temporally unique paths can be traversed in 5 rounds where exactly three $L$eft moves are taken?". For example, even though $L\rightarrow L\rightarrow R \rightarrow R \rightarrow L$ puts you in the exact same location as $R\rightarrow R\rightarrow L \rightarrow L \rightarrow L$, the 'history of the path' that led you to that same location was distinct. Therefore, these two sequences would each count towards the grand total.
To answer this question, you can imagine five empty slots: $\underline {\text{ }} \rightarrow \underline {\text{ }} \rightarrow \underline {\text{ } }\rightarrow \underline {\text{ } }\rightarrow \underline{\text{ }}$. There are 5 different slots for the first left $L_1$ to be placed...then there are 4 remaining different slots for a second left $L_2$ to be placed...then there are 3 remaining different slots for the third $L_3$ to be placed. IMPORTANTLY, the generation of this list does not respect the temporal requirement of our sequences (where round $n-1$ preceded round $n$). As such, the above list treats the following sequences as 1) distinct and 2) valid: $L_2 \rightarrow \underline {\text{ }} \rightarrow \underline {\text{ } }\rightarrow L_1 \rightarrow L_3$ and $L_3 \rightarrow \underline {\text{ }} \rightarrow \underline {\text{ } }\rightarrow L_2\rightarrow L_1$. Really, for the given $L$ configuration (an $L$ in the first, fourth, and fifth spot) the only valid path is: $L_1 \rightarrow \underline {\text{ }} \rightarrow \underline {\text{ } }\rightarrow L_2\rightarrow L_3$. To account for this inclusion of invalid paths, we need some sort of normalization routine. A given $L$ configuration of three $L$'s will have $3\times 2 \times 1=6$ variations. Using the above $3L$ configuration as an example, the $6$ variations of that particular $3L$ configuration in Round 5 are:
$L_1 \rightarrow \underline {\text{ }} \rightarrow \underline {\text{ } }\rightarrow L_2\rightarrow L_3$
$L_1 \rightarrow \underline {\text{ }} \rightarrow \underline {\text{ } }\rightarrow L_3\rightarrow L_2$
$L_2 \rightarrow \underline {\text{ }} \rightarrow \underline {\text{ } }\rightarrow L_3\rightarrow L_1$
$L_2 \rightarrow \underline {\text{ }} \rightarrow \underline {\text{ } }\rightarrow L_1\rightarrow L_3$
$L_3 \rightarrow \underline {\text{ }} \rightarrow \underline {\text{ } }\rightarrow L_2\rightarrow L_1$
$L_3 \rightarrow \underline {\text{ }} \rightarrow \underline {\text{ } }\rightarrow L_1\rightarrow L_2$
As such, to calculate the number of temporally unique (and valid) $3L$ paths, we perform the following operation: $\frac{5 \times 4 \times 3}{3\times 2 \times 1}$. Note, though, that this is equivalent to $\frac{5 \times 4 \times 3 \times (2 \times 1)}{(3\times 2\times 1)\times (2 \times 1)} = \frac{5!}{(3!)(2!)}$. So as it turns out, the binomial coefficient $\binom{5}{3}$ corresponds to the question: "How many temporally unique (and valid) paths can be traversed in 5 rounds where exactly three $L$eft moves are taken?"
