Trig Identity / Pythagorean Theorem confusion?

Question

I run into a problem when I'm trying to prove how $\tan^2x+1 = \sec^2x$, and $1+\cot^2x=\csc^2x$

I understand that $\sin^2x+\cos^2x = 1$. (To my understanding 1 is the Hypotenuse, please correct me if I'm wrong). If referring to a Pythagorean triangle, let's say a triangle where $a=3$, $b=4$, and $c=5$, or $a=\cos$ $b=\sin$ and $c=\text{hypotenuse}$.

$3^2 + 4^2 = 5^2$. Which is true and proves that this identity work. To my understanding, that is how this identity work.

However, when I try to make sense of the $\tan^2x+1 = \sec^2x$ and $1+\cot^2x=\csc^2x$ identity, using the triangle example from above, it doesn't work. For example, here's how I did it on paper,

$\tan^2x + 1 = {\sin^2x\over \cos^2x} + 1$, so I would get using the triangle above, ${4^2\over 3^2} + 1 = {16\over 9} + 1 = 2.777777778$

Now on the right hand side, $\sec^2x, = {1\over \cos^2x} = {1\over 3^2} = .1111111111$. The answer I get from $\tan^2x+1$ DOES NOT EQUAL the answer I get from $\sec^2x$. I think I may be misunderstanding a critical part here that I can't really pinpoint.

However, I do know that if I prove $\tan^2x+1 = \sec^2x$ using just the identity itself it does work, for example,

$\tan^2x+1 = {\sin^2x\over \cos^2x} + 1 = (\text{after some simplification}) = \sin^2x + {\cos^2x \over \cos^2x} = {1\over \cos^2x} = \sec^2x$.

The same issue happens with $1+\cot^2x=\csc^2x$.

To my understanding, $\sin^2+\cos^2=1$ is the same as $a^2+b^2=c^2$. Am I right or wrong? I think there is a huge concept that I am missing between the UNIT CIRCLE and just TRIANGLES.

Answer 1

Your issue is your understanding of the relationship between your basic trigonometry values and the sides of a triangle. You must keep in mind that the values of trigonometric functions are utilising the sides of your triangles in the following manner: $\sin(x) = \frac{opp}{hyp}$, $\cos(x) = \frac{adj}{hyp}$, and $\tan(x) = \frac{\sin(x)}{\cos(x)}$.

Let us use your example of a $3$, $4$, $5$ triangle to prove our identities.

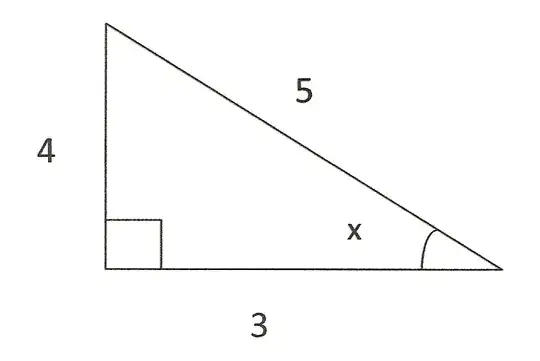Let us go ahead and figure out our values of $\cos(x)$, $\sin(x)$, and $\tan(x)$:

$$\sin(x) = \frac{4}{5}\\ \cos(x) = \frac{3}{5}\\ \tan(x) = \frac{\sin(x)}{\cos(x)} = \frac{\frac{4}{5}}{\frac{3}{5}} = \frac{4}{3}.$$

Now that we have figured out our values, we may plug them into our identities:

$$\sin^2(x) + \cos^2(x) = 1\\ \left(\frac{4}{5}\right)^2 + \left(\frac{3}{5}\right)^2 = 1\\ \frac{16}{25} + \frac{9}{25} = 1\\ \frac{25}{25} = 1$$

$\,$

$$1 + \cot^2(x) = \csc^2(x)\\ 1 + \left(\frac{1}{\frac{4}{3}}\right)^2 = \left(\frac{1}{\frac{4}{5}}\right)^2\\ 1 + \left(\frac{3}{4}\right)^2 = \left(\frac{5}{4}\right)^2\\ 1 + \frac{9}{16} = \frac{25}{16}\\ \frac{16}{16} + \frac{9}{16} = \frac{25}{16}\\ \frac{25}{16} = \frac{25}{16}$$

Attempt to prove $\tan^2(x) + 1 = \sec^2(x)$ by yourself to see if you fully understand.

---

A quick re-cap on the relationship of the three identities you proposed. Assuming you understand where $\sin^2(x) + \cos^2(x) = 1$ originated from, you should have no problems understanding where the next two identities originated from.

$1 + \cot^2(x) = \csc^2(x)$:

$$\sin^2(x) + \cos^2(x) = 1\\ \frac{\sin^2(x)}{\sin^2(x)} + \frac{\cos^2(x)}{\sin^2(x)} = \frac{1}{\sin^2(x)}\\ 1 + \cot^2(x) = \csc^2(x)$$

$\tan^2(x) + 1 = \sec^2(x)$:

$$\sin^2(x) + \cos^2(x) = 1\\ \frac{\sin^2(x)}{\cos^2(x)} + \frac{\cos^2(x)}{\cos^2(x)} = \frac{1}{\cos^2(x)}\\ \tan^2(x) + 1 = \sec^2(x)$$

Answer 2

The first identity works because $\frac{3}{5}^2+\frac{4}{5}^2=\frac{5}{5}^2$. When thinking of these trig ratios, you have to think of them in terms of both triangle sides you are interested in. Not merely one leg being equal to $\sin$, for example.

The beauty of the "unit" circle is that with the hypotenuse being $1$, in this case, we can think of the legs of the triangle being the actual value of $\sin$ and $\cos$, because the ratio of that length to $1$ is just that length.

You can workout the other identities if you express tan as $\frac{4}{3}$, $\csc$ as $\frac{5}{4}$, etc.