4

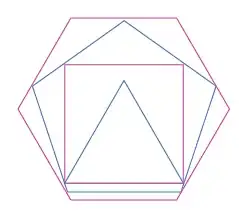
I want to build a figure that contains seven regular polygons, from a triangle up to a nonagon, where each n-sided polygon covers, with the minimal area possible, the n-1 sided one. An added restriction is that each of them should have a horizontal base.

With this figure constructed, I'd like to study its properties (mainly the side and area of each polygon, ideally expressed as a function of the triangle's side).

I wonder if there's a way to build this, either with a rule and a compass (unlikely, I presume) or by using a dedicated software program for this effect.

Thanks.

Miguel Farah
  • 49
  • 3
    Regular septagons and nonagons cannot be built from rule and compass, so that answers your first question. // When you say that each of them should have a horizontal base do you mean that the "bottom-most" edge of the polygons are all horizontal (and hence overlapping)? – Willie Wong Feb 23 '15 at 12:57
  • (Please scratch the word "hence" from the parenthetical of my previous comment.) – Willie Wong Feb 23 '15 at 13:03
  • Yes, I mean the bottom-most edge. –  Feb 23 '15 at 13:51

1 Answers1

6

To expland upon Willie Wong's question, is this what you mean by "each of them should have a horizontal base."?

          NestedRegPoly
Or, just to use $n=3,4,5,6$, this?
          NestedPoly3456
Joseph O'Rourke
  • 30,327
  • Regardless of the OP's original question: how did you generate the second picture? (In particular, did you analytically compute the vertices or did you just numerically found the solutions?) – Willie Wong Feb 23 '15 at 13:56
  • 2
    The second picture is the way I mean it - all polygons should have an horizontal bottom-most edge, but not actually the same side. See my own (extremely crude) rendering of the figure. –  Feb 23 '15 at 14:00
  • @WillieWong: Sorry to disappoint, but I did not code up anything formal. Consider those just approximate minimal-area enclosures; just drawings, really. – Joseph O'Rourke Feb 23 '15 at 14:02
  • @MiguelFarah: Thank you for clarifying your question. – Joseph O'Rourke Feb 23 '15 at 14:04