Need help with this integral $$\int\frac{1}{\cos x}dx$$ I know that the answer is $$\ln|\operatorname{tg} x+\sec x|$$ I tried transforming 1 into $\cos^2x + \sin^2x$ but it led to nothing. Need to solve it using simplest way without new variables and differential transformations.
Asked
Active
Viewed 180 times
0
-
3See this. – David Mitra Feb 23 '15 at 12:21
-
The goal of an indefinite integral is only to find the antiderivative. If you already know the antiderivative, try taking its derivative, and see how that simplifies down to $1/\cos(x)$. For simplicity, do this without the absolute value - usually that is found by doing a case analysis (or a substitution the leads to $\int 1/u,du$). – Carl Mummert Feb 23 '15 at 12:21
3 Answers
3
This is my way of finding this integral: $$\begin{align}\int \frac{1}{\cos{x}}dx =\int \frac{\cos{x}}{\cos^2{x}} dx= \int \frac{\cos{x}}{1-\sin^2{x}} dx\\ \text{substitution } \Big|\begin{array}{cc}\sin{x}=u \\ \cos{x}dx=du\end{array} \Big| \\= \int \frac{1}{1-u^2}du = \tanh^{-1}u +C= \tanh^{-1}(\sin{x})+C\end{align}.$$
m_gnacik
- 3,293
0
1/COSX=secx, multiply and divide it by secx+tanx you get int(secx^2+secxtanx)/(secx+tanx) dx which gives =log(tanx+secx)
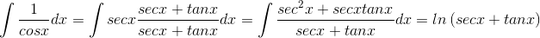
SA-255525
- 187
-
1Please format your answer using MathJax, a LaTeX-style system for typesetting math in answers. – Carl Mummert Feb 23 '15 at 12:22
-
1Consider writing your answer with mathjax. A small guide about it can be found here – Bman72 Feb 23 '15 at 12:22
0
Note that: $$ \dfrac{d}{dx} \tan x= \sec^2 x $$ and $$ \dfrac{d}{dx} \sec x= \sec x \tan x $$ so that: $$ d(\tan x +\sec x)= \dfrac{\tan x +\sec x}{\cos x} dx $$ and: $$ \dfrac{d(\tan x +\sec x)}{\tan x +\sec x}=\dfrac{dx}{\cos x} $$ so, integrating you have the result.
Emilio Novati
- 62,675