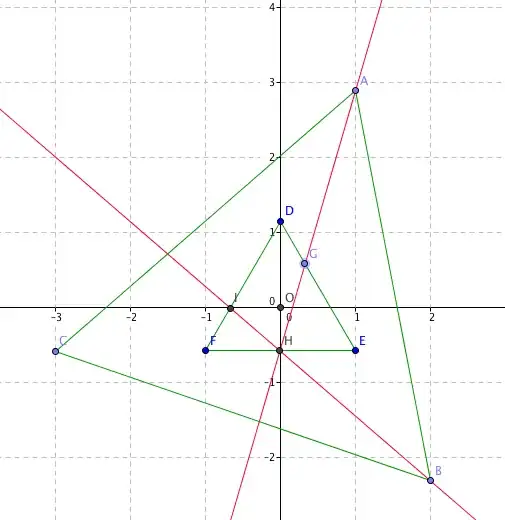
I'll approach this problem by relating the congruence of $\overline{DG}$, $\overline{EH}$, $\overline{FI}$ to how (or whether) $\overleftrightarrow{AG}$ contains $H$, $\overleftrightarrow{BH}$ contains $I$, and/or $\overleftrightarrow{CI}$ contains $G$.
My tool of choice is my Extended Ceva's Theorem, introduced in this answer, but reformulated here:
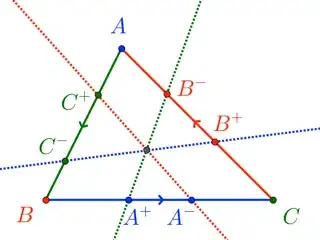
Extended Ceva's Theorem. Lines $\overleftrightarrow{A^+B^{-}}$, $\overleftrightarrow{B^+C^-}$, $\overleftrightarrow{C^+A^-}$ through the edges of $\triangle ABC$ concur if and only if
$$\alpha^+ \beta^+ \gamma^+ + \alpha^-\beta^-\gamma^- + \alpha^+\alpha^- + \beta^+\beta^- +\gamma^+\gamma^- = 1 \tag{$\star$}$$
where
$$\alpha^+ := \frac{|BA^+|}{|A^+ C|} \qquad \beta^+ := \frac{|CB^+|}{|B^+A|} \qquad \gamma^+ := \frac{|AC^+|}{|C^+B|}$$
$$\alpha^- := \frac{|CA^-|}{|A^- B|} \qquad \beta^- := \frac{|AB^-|}{|B^-C|} \qquad \gamma^- := \frac{|BC^-|}{|C^-A|}$$
Now for the problem at hand.

Extend the edges of $\triangle DEF$ to meet the sides of $\triangle ABC$ at points $P_i$ and $Q_i$; by symmetry, there are $p$ and $q$ such that
$$
\frac{|BP_a|}{|P_aC|} = \frac{|CP_b|}{|P_bA|} = \frac{|AP_c|}{|P_cB|} = p \qquad
\frac{|CQ_a|}{|Q_aB|} = \frac{|AQ_b|}{|Q_bC|} = \frac{|BQ_c|}{|Q_cA|} = q
$$
Moreover, extend $\overline{AG}$, $\overline{BH}$, $\overline{CI}$ to meet the edges of $\triangle ABC$ at $A^\prime$, $B^\prime$, $C^\prime$, and define
$$\alpha := \frac{|CA^\prime|}{|A^\prime B|} \qquad \beta := \frac{|AB^\prime|}{|B^\prime C|} \qquad \gamma := \frac{|BC^\prime|}{|C^\prime A|}$$
By the ECT with substitutions
$$A^+ \to P_a \qquad A^-\to A^\prime \qquad B^+\to C \qquad B^-\to Q_b \qquad C^+\to A \qquad C^-\to C^\prime$$
so that
$$\alpha^+ = p \qquad \beta^+ = \gamma^+ = 0 \qquad \alpha^- = \alpha \qquad
\beta^- = q \qquad \gamma^- = \gamma$$
we have that $\overleftrightarrow{CI}$ contains $G$ (which is to say that $\overleftrightarrow{AG}$, $\overleftrightarrow{CI}$, $\overleftrightarrow{DE}$ concur at $G$) if and only if
$$1 = \alpha\;(\; p + q \gamma \;) \tag{$1$}$$
Likewise, $\overleftrightarrow{AG}$ contains $H$ if and only if
$$1 = \beta\;(\; p + q \alpha \;) \tag{$2$}$$
and $\overleftrightarrow{BH}$ contains $I$ if and only if
$$1 = \gamma\;(\;p + q \beta \;) \tag{$3$}$$
Now, the problem asserts that $\overleftrightarrow{AG}$ and $\overleftrightarrow{BH}$ contain $H$ and $I$, respectively; therefore, $(2)$ and $(3)$ hold. The problem also asserts that $\overline{DG}\cong\overline{FI}$, so that $\overline{AC^\prime}\cong\overline{CB^\prime}$, which implies $\alpha = \gamma$. Provided that $p\neq 0$, we may conclude that $\alpha = \beta = \gamma$, that all three concurrencies hold, and that $\overline{DG}\cong\overline{EH}\cong\overline{FI}$.
Note. When $p=0$, the figure is such that $\overleftrightarrow{DF}$ contains $A$ (and so forth for other edge-lines and vertices). Here, we need not assume $\overline{DG}\cong\overline{FI}$, as the fact that $\alpha = \gamma$ (and therefore that congruence) follows from assuming $(1)$ and $(2)$ (with $\beta \neq 0$). There's no guarantee, though, that $(1)$ holds. @Ewan's answer gives a case in which it doesn't.
Note. When $q=0$, the figure is such that $\overleftrightarrow{DE}$ contains $A$ (and so forth). By the problem's construction, any point $G$ on $\overline{DE}$ causes $H$ and $E$ to coincide, whereupon $I$ and $F$ also coincide; to satisfy the condition $\overline{DG}\cong\overline{FI}$, we must have that $G$ and $D$ coincide, as well. This, obviously, satisfies all the concurrencies and gives that $\alpha = \beta = \gamma$.