Gradient of $X \mapsto a^T X b$ when $X$ is symmetric

Question

For matrix $X \in \Bbb R^{n \times n}$, $a \in \Bbb R^n$, and $b \in \Bbb R^n$, I know the following holds

$$\nabla_X \left( a^T X b \right) = a{b^T}$$

However, it seems that if $X$ is a symmetric matrix ($X \in \Bbb S^n$), then

$$ \nabla_X \left( {a^T} X b \right) = \frac{1}{2}(a{b^T} + {b}a^T) $$

How to understand it? If $X \in \Bbb S^n$, then the dimension of $X$ is $\frac{n(n+1)}{2}$. Why should we get $n^2$ elements after differentiation?

Answer 1

Define a non-standard symmetrizing operation for a square matrix ($A$) as $$ {\rm nsym}(A) = A + A^T - I\circ A $$ Now suppose that you have determined the differential of some scalar-valued function $f(X)$ to be $$ df = A:dX $$ Later you are told that $X$ is constrained to be symmetric. How does such a constraint modify the unconstrained result? The answer is to use nsym() $$ df = {\rm nsym}(A):dX $$ Applying this to the current problem yields $$ \frac{\partial f}{\partial X} = ab^T + ba^T - {\rm diag}(a\circ b) $$ A lot of people mistakenly apply the standard symmetrizing operator, i.e. $$ {\rm sym}(A) = \frac{1}{2}(A + A^T) $$ in this situation.

BTW, if the constraint is to be diagonal, then the symmetrizing operation to apply is $$ {\rm dsym}(A) = I\circ A $$

Answer 2

It is the notation what causes confusion!

If we define \begin{align*} \phi\,\colon\, &\mathbb{R}^{n\times n}\to\mathbb{R}\\ &Y\mapsto a^TYb \end{align*} it is certainly true that $$ \frac{\partial\phi}{\partial x_{ij}}(Y) = a_ib_j=(ab^T)_{ij} $$

irrespectively of whether $Y$ is symmetric or not. This fact is easily verified by observing that $\phi$ is linear and therefore equal to its differential, i.e., $$ D\phi(Y) = \phi\qquad\text{or}\qquad D\phi(Y)(M) = a^TMb\quad (M\in\mathbb{R}^{n\times n}) $$ This allows us to write $$ \frac{\partial\phi}{\partial x_{ij}}(Y) = D\phi(Y)(E_{ij}) = a^TE_{ij}b = a_ib_j, $$ which corresponds to your partial derivative w.r.t. $X$. Equivalently $$ \nabla\phi(Y) = ab^T. $$ However, there is another interpretation for the same notation, which becomes clear if we name the functions we use. Consider the following diagrams

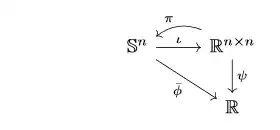
where $\iota$ is the natural embedding, $\pi$ the projection $\pi(Y)=(1/2)(Y+Y^T)$, $\phi$ is as above, $\bar{\phi}$ is just the restriction of $\phi$ and $\psi$ is given by $$ \psi(Y) = a^T(Y+Y^T)b/2. $$ These diagrams aren't equivalent. In fact, the one on the left does not commute with regards to $\pi$, while the one on the right fully commutes.

Now, if we reason as we did above for $\phi$, this time for $\psi$, we get $$ \frac{\partial\psi}{\partial x_{ij}}(Y) = D\psi(Y)(E_{ij}) = \psi(E_{ij}) = a^T(E_{ij}+E_{ji})b/2 = (a_ib_j+a_jb_i)/2, $$ and therefore $$ \nabla\psi(Y) = (ab^T + ba^T)/2. $$ This explains why there appears to be two different partial derivatives, it is just that we are taking derivatives of two different functions and the (simplified) notation (which disregards function names) cannot distinguish between them.