What is the proof that the two below are equal?

Question

Can you help me to prove the following equality ?

Answer 1

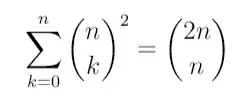
Let us first prove the Vandermonde identity : $\forall\left(n,m,k\right)\in\mathbb{N}^{3}$ $$\sum_{j=0}^{k}\begin{pmatrix}m\\ j \end{pmatrix}\begin{pmatrix}n\\ k-j \end{pmatrix}=\begin{pmatrix}m+n\\ k \end{pmatrix}\,\,\,\,\,\left(1\right).$$

We have for all $x\in\mathbb{R}$ $$\sum_{k=0}^{m+n}\begin{pmatrix}m+n\\ k \end{pmatrix}x^{k}=\left(1+x\right)^{m+n}=\left(1+x\right)^{m}\left(1+x\right)^{n}=\left(\sum_{j=0}^{m}\begin{pmatrix}m\\ j \end{pmatrix}x^{j}\right)\left(\sum_{k=0}^{n}\begin{pmatrix}n\\ j \end{pmatrix}x^{k}\right)=\sum_{k=0}^{m+n}\left(\sum_{j=0}^{k}\begin{pmatrix}m\\ j \end{pmatrix}\begin{pmatrix}n\\ k-j \end{pmatrix}\right)x^{k},$$ $$\begin{pmatrix}m+n\\ k \end{pmatrix}x^{k}=\sum_{j=0}^{k}\begin{pmatrix}m\\ j \end{pmatrix}\begin{pmatrix}n\\ k-j \end{pmatrix}x^{k}.$$ For $x=1$ , one obtains the result.

Then, for $m=k=n$ in $\left(1\right)$ , it comes

$$\sum_{k=0}^{n}\begin{pmatrix}n\\ k \end{pmatrix}^{2}=\begin{pmatrix}2n\\ n \end{pmatrix}.$$

Answer 2

A proof of it is on Wikipedia here.

Just for kicks, here's a combinatorial proof. The right hand side is the number of ways to choose $n$ objects from a set of $2n$ objects.

If we split up the $2n$ objects as such: $1,2,\ldots,n | n+1, \ldots, 2n $, then we see that in order to pick $2n$ objects in total, we have to pick $k$ from the first $n$, and $n-k$ from the second set of $n$. Summing over $k$ yields $$ \sum\limits_{k=0}^n \binom{n}{k}\binom{n}{n - k} = \sum\limits_{k = 0}^n \binom{n}{k}^2 $$

Since the two values count the same thing, they must be equal.