What mistake am I making when trying to apply Fermat's little theorem?

Question

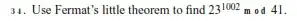
This is a problem from Discrete Mathematics and its Applications enter image description here

This is Fermat's little theorem from https://www.youtube.com/watch?v=w0ZQvZLx2KA, enter image description here

Here is my work so far

First 41 is prime and $41\not\mid23$

So $23^{40}\equiv1\pmod {41}$

From my observation that $1002/40 = 25$, I rooted both sides of $23^{40}\equiv1$ by $25$

(allowed to so by Congruence product rule, Divisibility for 7)
Here is what am I left with $$23^{1000}\equiv1\pmod {41}$$ Then I used the fact that $1002 \mod 40 = 2$ and the congruence product rule to get
$$23^{1002}\equiv 23^2\pmod {41}$$ Then with this property from my book enter image description here

I know that $23^{1002}\mod 41 = 23^2 \mod 41$. $23^2\mod 41$ from my calculator is $18$ so that be my final answer as well.
But when I checked my answer on http://www.mathcelebrity.com/modexp.php?num=+23%5E1002+mod+41&pl=Modular+Exponentiation, the correct answer was 37.

Does anyone know I did wrong -either arithmetically or applying theorems?

Your calculator misled you when you found $23^2(\mod41)$ – user84413 Feb 14 '15 at 19:38 — user84413, Feb 14 '15 at 19:38
Actually I think I mislead myself haha – committedandroider Feb 14 '15 at 20:04 — committedandroider, Feb 14 '15 at 20:04

score 2 · Accepted Answer · answered Feb 14 '15 at 19:51

2

Hint $\ {\rm mod}\ 41\!:\,\ 23^2 \equiv (-2\cdot9)^2 \equiv\, 4(\overbrace{-1}^{\large81}) \equiv 37.\ $ Trust your brain more than your calculator.

answered Feb 14 '15 at 19:51

Bill Dubuque

272,048

How did you get 23$^2$≡(−2⋅9)$^2$? – committedandroider Feb 14 '15 at 20:05
@com ${\rm mod}\ 41!:\ 23\equiv 23-41\equiv -18.\ $ Generally modular arithmetic is easier with least magnitude reps, here $,|{-}18| < 23.\ $ Recall also the use of $,-1,$ vs. $,m!-!1\pmod m\ \ $ – Bill Dubuque Feb 14 '15 at 20:06

score 0 · Answer 2 · answered Feb 14 '15 at 19:56

0

$$23^2 \equiv (20+3)^2=20*20+20*2*3+9=\\ = 40*10+40*3+9 \equiv -10-3+9=-4=37 \pmod{41}$$

answered Feb 14 '15 at 19:56

N. S.

132,525

What mistake am I making when trying to apply Fermat's little theorem?

2 Answers2