How to prove this following trigonometric equation?

Question

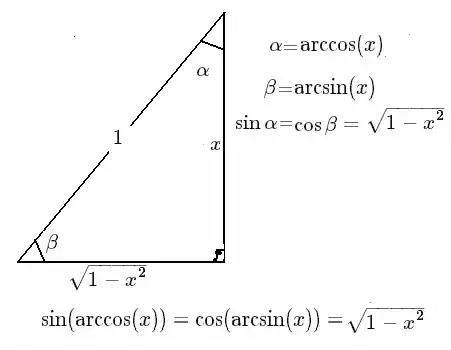
How can I prove the equation below? $$\sin(\arccos(x))=\cos(\arcsin(x)) = \sqrt{1-x^2}$$ $$-1\leq{x}\leq1$$

Answer 1

It follows from the Pythagorean identity $\sin^2 x + \cos^2 x = 1$, that for $-1 \leq x \leq 1$, $$\cos x = \sqrt{1 - \sin^2 x}.$$

Therefore $$\cos(\arcsin x) = \sqrt{1 - \sin^2(\arcsin x)} = \sqrt{1 - x^2},$$ because $\sin(\arcsin x) = x$ for every $x \in [-1, 1]$.

The other one is very similar, can you finish the exercise?

Answer 2

You can use the following fact:

$$\sin^2 (x) + \cos^2 (x) = 1$$

Let's define $y=\arccos x$. Thus we have:

$$\sin^2 y + \cos^2 y = 1 \implies \\ \sin^2 y + x^2 = 1 \implies \\\sin^2 y = 1-x^2 \implies \\ \sin y = \sqrt{(1-x^2) } \implies \\\sin(\arccos x) = \sqrt{(1-x^2)}$$

Notice that $\cos(\arccos x ) = x$ for every $x \in [-1, 1]$.

Answer 3

Just follow the definition: Ratio of sides of a right angled triangle.

Answer 4

Start from the identity $\sin^2 y+\cos^2 y=1$ where $y=\arccos x$ this leads $\sin^2\arccos x+x^2=1$ (because $\cos \arccos x=x$) and thus the identity for sine. Same with cosine