Just Some Nerdy Teen made an interesting comment (in a now deleted answer) :
"You should put ExpIntegralEi(rho*log(x)) instead of LogIntegral(x^rho)".
The observed curve was indeed an artifact coming from the use of the logarithmic instead of the exponential integral!
The problem is that the logarithmic integral requires (at least) the evaluation of the logarithm of its parameter $x^\rho\,$ but $\,\log(x^\rho)\,$ will differ from $\,\rho\,\log(x)\,$ for $\rho\gg 1\,$ (CAS use simply the principal branch of the logarithm!).
The solution indicated by JSNT is to use the relation $\;\displaystyle\mathrm{li}(z)=\mathrm{Ei}(\ln z)\;$ with $\,\mathrm{Ei}\,$ the exponential integral and rewrite your sum for the $n$ first complex zeros (with positive imaginary part) as :
$$\tag{1} S_n(x):=\sum_{i=1}^n{\mathrm{Ei}(\rho_i\ln x)}$$
(different 'traps' to avoid while evaluating the explicit formula(s) conclude this answer)
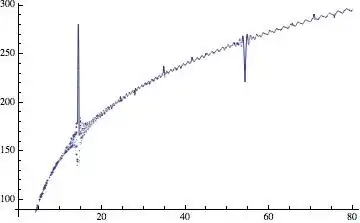
Let's compare the result using $\,\mathrm{Ei}(\ln x^{\rho_i})\,$ (your picture with $\,n=100$) :
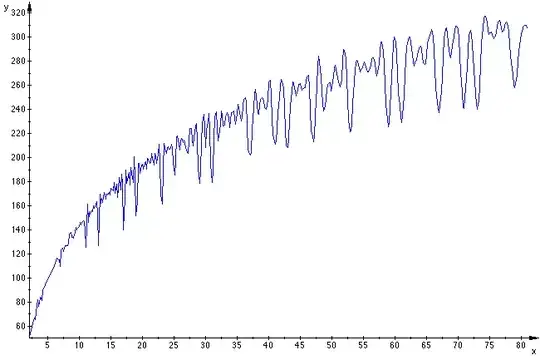
with the actual result for $(1)$ :
Riemann's explicit formula restrained to the $\,(2)n\,$ 'smallest' non trivial zeros is (for $x>1$ and using $\,\mathrm{Ei}(\overline{\rho_i}\ln x)=\overline{\mathrm{Ei}(\rho_i\ln x)}$ for the $n$ first complex zeros with negative imaginary part): $$\tag{2}\Pi_{n}(x)=\mathrm{Ei}(\ln(x))-\sum_{k=1}^\infty \mathrm{Ei}(-2k\,\ln x)-2\,\Re\,S_n(x)$$ may then be used
to visualize the Riemann Prime Counting Function $\Pi$.
For $n=100$ we get :
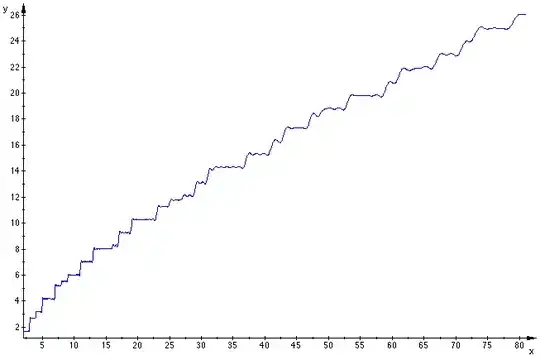 that we may compare to the actual $\;\displaystyle\Pi(x)=\sum_{p^k<x}\frac 1k$ :
that we may compare to the actual $\;\displaystyle\Pi(x)=\sum_{p^k<x}\frac 1k$ :
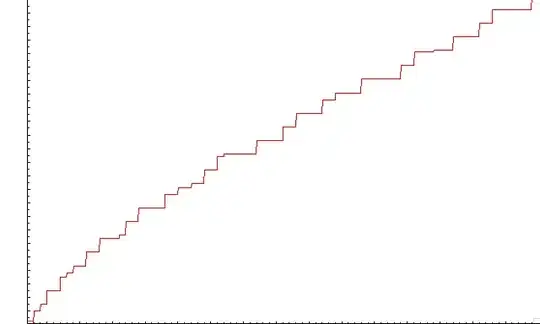
The artifact was thus eliminated but, out of curiosity, can we approximate it?
The actual error is of course given by the evaluation of (with $[x]$ the nearest integer) :
\begin{align}
\tag{3} \Delta_n(x)&:=\Re\sum_{i=1}^n \mathrm{Ei}(\ln x^{\rho_i})-\mathrm{Ei}(\rho_i\ln x)\\
\tag{4} &=\Re\sum_{i=1}^n \mathrm{Ei}\left(\frac{\ln x}2+\left(\frac{\Im\rho_i\ln x}{2\pi}-\left[\frac{\Im\rho_i\ln x}{2\pi}\right]\right)2\pi\,i\right)-\mathrm{Ei}(\rho_i\ln x)\\
\end{align}
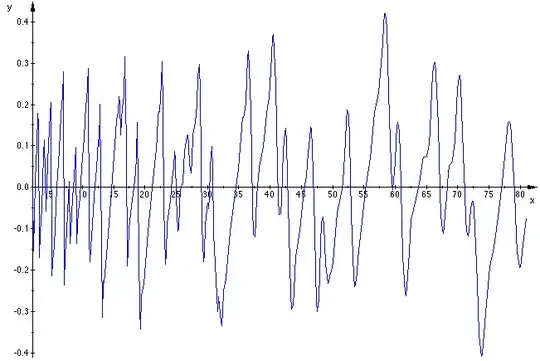
Which gives nearly your initial picture (observe the bounds on my second picture suggesting to neglect the right part :$\,\Re\sum_{i=1}^n\mathrm{Ei}(\rho_i\ln x)\,$). One could think at neglecting the imaginary part in the first term and write $\:\Delta_n(x)\approx\Re\sum_{i=1}^n \mathrm{Ei}\left(\frac{\ln x}2\right)=n\,\mathrm{li}(x^{1/2})$. This corresponds to your conjecture but only if divided by a value near of $2$.
A more precise result is obtained with the average value of $\;\mathrm{Ei}\left(\frac{\ln x}2+ti\right)$ for $t$ in $(-\pi,\pi)\,$ which can be done using integration by parts to get $\;\displaystyle\int \mathrm{Ei}(x) dx= x\mathrm{Ei}(x)-e^x\;$ and the better approximation :
$$\tag{5}\Delta_n(x)\approx \left.-\,\frac n{2\pi}\,i\,\left(\frac{\ln x}2+ti\right)\mathrm{Ei}\left(\frac{\ln x}2+ti\right)\right|_{t=-\pi}^\pi $$
illustrated by following figure with $(5)$ in red and the OP's approximation $\;n\,\mathrm{li}(x^{1/2})/2$ at the bottom:
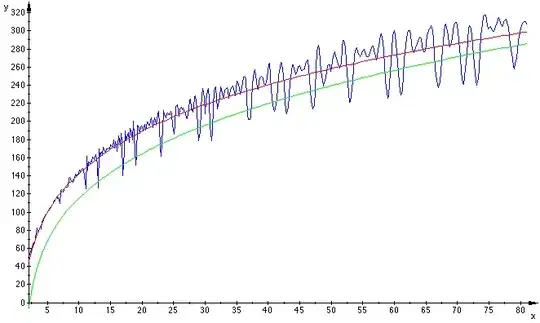
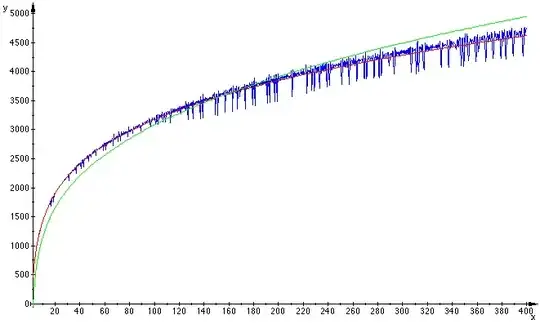
With $n=1000$ zeros (instead of $100$) and a larger range the approximation $(5)$ seems the only one to remain reliable :
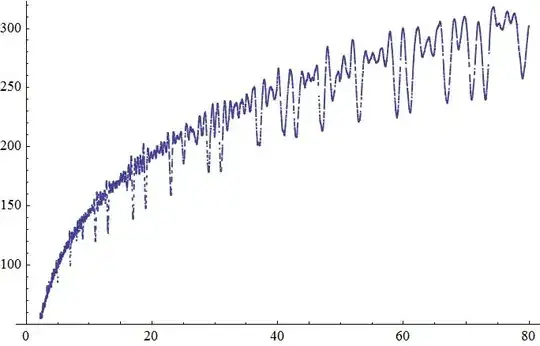


 that we may compare to the actual $\;\displaystyle\Pi(x)=\sum_{p^k<x}\frac 1k$ :
that we may compare to the actual $\;\displaystyle\Pi(x)=\sum_{p^k<x}\frac 1k$ :


