0

I have a question for my exam and I find it hard to understand.

I have to prove that the following formula is logically valid:

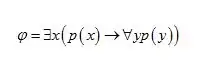
Example

The professor told me to "push" all the symbols inside the brackets, and use the deduction theorem.

But I don't know how to do it, because I can't find the identities to push the "exist" symbol inside the brackets.

Your help is appriciated, thank you.

Alan

Alan
  • 2,791

2 Answers2

2

Assume $\forall yp(y)$. Then $p(x)\to\forall yp(y)$ is true for any $x$. If on th eother hand $\neg \forall yp(y)$, then $\exists y\neg p(y)$. Let $x$ be such an $y$ then again $p(x)\to\forall yp(y)$ is true, this time because the antecedent is false.

Hagen von Eitzen
  • 374,180
1

Perhaps he meant something like this:

\begin{align} \exists x\ \big(p(x) &\to \forall y\ p(y)\big) \\ \exists x\ \big(\neg p(x) &\lor \forall y\ p(y)\big) \\ \big(\exists x\ \neg p(x)\big) &\lor \big(\forall y\ p(y)\big) \\ \neg\big(\forall x\ p(x)\big) &\lor \big(\forall y\ p(y)\big) \\ \big(\forall x\ p(x)\big) &\to \big(\forall y\ p(y)\big) \\ \end{align}

Please note that the step from line 2 to 3 is not an equivalence, if the universe is empty, then line 3 is true, but line 2 is false.

I hope this helps $\ddot\smile$

dtldarek
  • 37,381