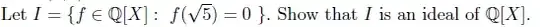I am trying to show that
I have said:
f=0 is in I so I is non-empty.
Let $f,g$ be members of $I$
$(f+g)(\sqrt5)=f(\sqrt5)+g(\sqrt5)=0+0=0 ==> f+g ∈ I$ so I is closed under addition
Let $g∈Q[x], f ∈ I$
$fg(\sqrt5)=f(\sqrt5)g(\sqrt5)=0*g(\sqrt5)=0 ==> fg ∈ I $ so I closed under multiplication from R.
Is this sufficient to show that I is an ideal?
Let's rephrase it slightly to gain a little more insight. Let $\,\ell(f) = f(\sqrt{5})\,$ be the map that evaluates $\,f(x)\,$ at $\,x = \sqrt{5}.\,$ Note that it is a ring hom: $\ \ell(f\pm g) \,=\, \ell f \pm \ell g ,\, $ and $\ \ell(fg) = (\ell f)\,(\ell g).\ $
More generally let $\,\ell \,$ be any ring hom and let $I$ be its kernel, i.e. all $f$ such that $\,\ell f = 0.\,$
Then $\,f,g \in I\,\Rightarrow\, \ell f,\,\ell g=0\,\Rightarrow\ \ell(f\pm g) = \ell f \pm\ell g = 0\pm0 = 0\ \Rightarrow\, f\pm g\in I,\ $ and
further $\ \ell(fh) = \ell f\, (\ell h) = 0\cdot \ell h = 0,\ $ so $\,fh\in I.\,$ Thus the kernel of a ring hom is an ideal.
Likewise, many ideals arise naturally as kernels of ring homomorphisms.
Remark $\ $ This raises an important question: why is the evaluation map a ring hom? Have you proved that yet? Note that this is not true for any ring, since, if so, evaluating $\, ax = xa $ at $\,x = b\,$ shows $\,ab = ba\,$ so the coefficient ring is commutative. In fact, this necessary condition is also sufficient for evaluation to be a ring hom. You should prove this at some point, since it helps to understand essential properties of polynomial rings $\,R[x]\,$ (as universal $R$-algebras).
You've shown it to be closed to multiplication from the ring and to additions. Can you show it's also an additive subgroup?
The usual definition of an ideal is that it is an additive subgroup of $R$ stable under multiplication by elements of $R$.
Your first point does not in itself show the first part, as an additively closed subset might not be a subgroup.
It is however possible that you have either an unusual defintion or a lemma that allows for your proof. The point is that by the multiplicative closedness you get additve inverses "for free" as $-g = (-1)g$.
A common criterion to show that something is an ideal is to show for the additive part that $f-g \in I$ for $f,g \in I$; that is using a common criterion for a non-empty subset being a subgroup.
