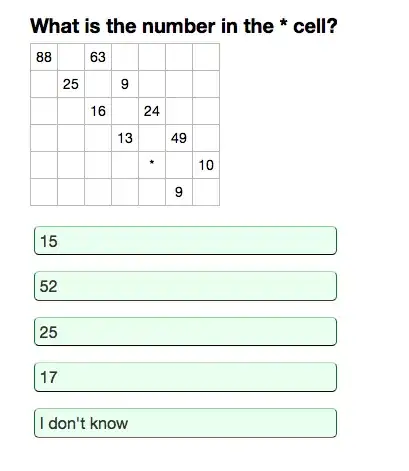
It is possible that 25 is the correct answer since I guessed (educated guess) that and got a predication of 170 IQ (obviously not accurate)
I saw that
63 + 25 = 88 and
16 + 9 = 25
but then that breaks apart the lower you go.
Any ideas?
I saw that nine was repeated so maybe 25 would also be repeated?