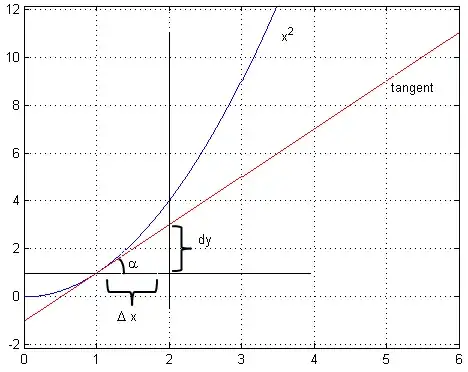
I was thinking about, of the derivative as an operator, like $\frac{dy}{dx}$, and i am having trouble thinking on the things you do in courses of differential equations, with the $dx, dy$, like passing them around from one side of the equation, and to the other, with apparently no problem, i don't worry much about it, because in a lot of physics texts they do that, and it works,
But when i ask about WHY?, they say, don't worry for now, if it works, don't worry.
Once i ask a mathematician, why and he refereed to "high level math" subjects and books, and i couldn't get all he said, so i am looking for a "formal" simplest answer to "Why can we do Algebra with the Differential operators, why does it work, and until what point does it works"