Is there formula for the volume of a hexahedron?

Question

If there a closed form expression for the volume enclosed by 8 points $(x_1, y_1, 0)$, $(x_2, y_2, 0)$, $(x_3, y_3, 0)$, $(x_4, y_4, 0)$, $(x_1, y_1, h_1)$, $(x_2, y_2, h_2)$, $(x_3, y_3, h_3)$ and $(x_4, y_4, h_4)$? I think it's called a hexahedron or 3D-trapezium, not sure. None of the first 4 points are the same as any other, and the last four points line in a plane.

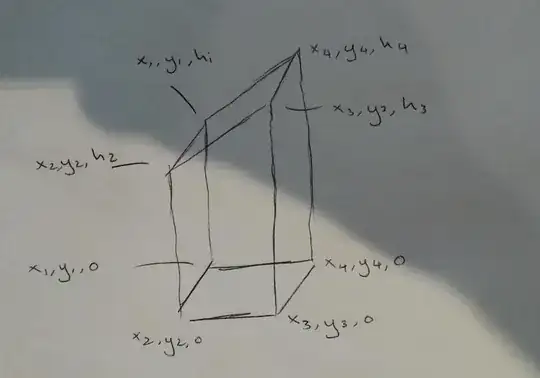
Here's a picture:

$(x,z)=(0,0)$ is a line (the y-axis) in three-dimensional space, not a plane. — KSmarts, Feb 10 '15 at 17:27
Even if you really mean a plane, what exactly do you mean by a space "bounded by" 4 points and a plane? You need to explain much more precisely what you have in mind. Also, two of your "four" points seem to be identical. — Old John, Feb 10 '15 at 17:32
Still not sure what this is: what if your last four points do not lie in a plane? — Old John, Feb 10 '15 at 17:36
@OldJohn edit again thanks. It's effectively a column, with a quadrilateral base, chopped off at the top at some angle. I've added a picture. — nickponline, Feb 10 '15 at 17:43
If the upper face is plane (as I suppose), $h_4$ is non independent from $h_1,h_2,h_3$. I'm right? — Emilio Novati, Feb 10 '15 at 17:53
Possible duplicate of What is the enclosed volume of an irregular cube given the x,y,z coordinates of the 8 corners? — ccorn, Jul 16 '17 at 17:03

achille hui · Accepted Answer · 2015-02-11T09:25:22.040

Instead of $4$ pairs of points, let's look at the case with $3$ pairs of points first.

Let $H = \big\{ (x,y,h) \in \mathbb{R}^3 : h \ge 0 \big\}$ be the upper half-space.
For any $p = (x,y,h) \in H$, let $\tilde{p} = (x,y,0)$ be its projection on the $xy$-plane.

Given any $3$ points $p_1, p_2, p_3\in H$ whose projections $\tilde{p}_1$, $\tilde{p}_2$, $\tilde{p}_3$ bounding a triangle in the $xy$-plane in counter-clockwise orientation, consider the convex hull formed by following $6$ vertices $p_1, p_2, p_3, \tilde{p}_1, \tilde{p}_2, \tilde{p}_3$. The resulting polyhedron is a truncated triangular prism. To compute its volume, we split it into $3$ tetrahedra:

$$\tilde{p}_1, \tilde{p}_2, \tilde{p}_3, p_3;\quad \tilde{p}_1, \tilde{p}_2, p_3, p_2;\quad\text{ and }\quad \tilde{p}_1, p_2, p_3, p_1$$ We find $$\begin{align} \verb/Volume/ &= \frac16 \begin{vmatrix} 1 & x_1 & y_1 & 0\\ 1 & x_2 & y_2 & 0\\ 1 & x_3 & y_3 & 0\\ 1 & x_3 & y_3 & h_3\\ \end{vmatrix} + \frac16 \begin{vmatrix} 1 & x_1 & y_1 & 0\\ 1 & x_2 & y_2 & 0\\ 1 & x_3 & y_3 & h_3\\ 1 & x_2 & y_2 & h_2\\ \end{vmatrix} + \frac16 \begin{vmatrix} 1 & x_1 & y_1 & 0\\ 1 & x_2 & y_2 & h_2\\ 1 & x_3 & y_3 & h_3\\ 1 & x_1 & y_1 & h_1\\ \end{vmatrix}\\ \\ &= \frac{h_1+h_2+h_3}{6}\begin{vmatrix} 1 & x_1 & y_1\\ 1 & x_2 & y_2\\ 1 & x_3 & y_3\\ \end{vmatrix} \end{align} $$

For the truncated quadrilateral prism at hand, we can split it into two truncated triangular prisms. Up to a sign, the volume you seek will be equal to: $$\verb/Volume/ = \frac{h_1+h_2+h_3}{6}\begin{vmatrix}1 & x_1 & y_1\\1 & x_2 & y_2\\1 & x_3 & y_3\end{vmatrix} + \frac{h_1+h_3+h_4}{6}\begin{vmatrix}1 & x_1 & y_1\\1 & x_3 & y_3\\1 & x_4 & y_4\end{vmatrix} $$

score 2 · Answer 2 · answered Feb 10 '15 at 18:15

Whenever you have 3D-object like this, split the object into tetrahedrons, since there is a formula for the volume. If a tetrahedron has corners $a,b,c,d\in\mathbb R^3$, then its volume is given by \begin{align*} \frac{1}{6}\cdot\det\left|(a-d,b-d,c-d)\right|. \end{align*} Then sum the volumes of the tetraedrons up, and you are done.

Is there formula for the volume of a hexahedron?

2 Answers2