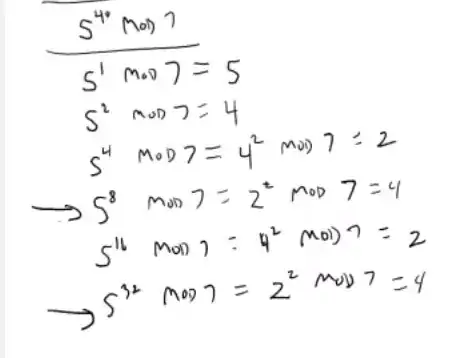2

I am watching a youtube video on modular exponentiation https://www.youtube.com/watch?v=sL-YtCqDS90

Here is author's work

enter image description here

In this problem, the author was trying to calculate $5^{40}$

He worked the powers of 5 by 2 until he go to the largest exponent that was less than 40, 32. He then reasoned that $5^{40}$ mod 7 = $5^{32}$ mod 7 * $5^ 8$ mod 7. Does anyone know where he got this property from? I know that there is an exponent property that would state $5^{40}$ = $5^{32}$ * $5 ^ 8$ (from http://hotmath.com/hotmath_help/topics/properties-of-exponents.html ) but can someone show how to get from that one to the mod version property? I tried looking it up but couldn't find it.

committedandroider
  • 1,884

5 Answers5

1

The aspect you're puzzled by, $(5^{40} \bmod 7) \equiv (5^{32} \bmod 7)(5^{8} \bmod 7) \pmod 7$, is really the same process that has been used through the whole squaring process that preceded it, where (for example) we had $(5^{32} \bmod 7) \equiv (5^{16} \bmod 7)(5^{16}\bmod 7) \pmod 7$.

Essentially it is the same property that you are probably familiar with from modular arithmetic in general. For example, consider calculating $(20\times 15) \bmod 7 $. We can take the $\bmod 7$ value of each: $20 \equiv 6 \bmod 7$ and $15 \equiv 1 \bmod 7$ - and use those values to calculate the result $(6 \times 1) = 6 \equiv 6 \bmod 7$. And to show that is truly the $\bmod 7$ value of the original multiplication, we can drop back into the $20=7k+6$ type representation and prove out that all the multiples of $7$ can be ignored in the multiplication process. And if we want to in this case, we can even check that $300-6$ is indeed divisible by $7$.

So all we're looking at there is a standard property of modular arithmetic - the congruence classes multiply together consistently.

All numbers $n$ such that $n \equiv k \bmod m$ are in the same congruence class $\bmod m$ . For example, $\{2,9,16,23,30,37, \ldots\}$ are all in the same congruence class $\bmod 7$, identified by the non-negative member of the class less than than the modulo number - in that case, $2$. Still working modulo $7$, if we multiply any member of congruence class $2$ by any member of congruence class $4$, the answer will be in congruence class $1$.

Joffan
  • 39,627
  • What do you mean by congruence classes? I've heard of congruency in that a is congruent to b modulo m if m divides a - b. – committedandroider Feb 10 '15 at 18:51
  • All numbers $n$ such that $n \equiv k \bmod m$ are in the same congurence class $\bmod m$ . For example, ${2,9,16,23,30,37, \ldots}$ are all in the same congruence class $\bmod 7$, identified by the non-negative member of the class less than than the modulo number - in that case, $2$. – Joffan Feb 10 '15 at 18:56
  • Oh Ok. That makes sense. How do you get from (20mod7)(15mod7) to ((6×1)mod7)? Did you do the actual 20 * 15 operation? – committedandroider Feb 10 '15 at 19:04
  • No, I took the mod of each of 20 and 15 first, then multiplied together the smaller numbers. Afterwards I mention that you can check the full result for those two (rather small) numbers. – Joffan Feb 10 '15 at 19:07
  • If you apply that rule, abmodm=((amodm)(bmodm))mod m, shouldn't you get $5^{40}$mod 7 = ($5^{32}$mod 7) ($5^8$ mod 7) mod 7. For your answer isn't there supposed to be an outer mod 7 on the right side as well? – committedandroider Feb 13 '15 at 22:03
  • Perhaps I should use \equivs, $(5^{40} \bmod 7)\equiv (5^{32}\bmod 7)(5^{8}\bmod 7)$, with "$\bmod 7$" the implied type of equivalence we're looking at. – Joffan Feb 13 '15 at 22:18
  • Oh ok. For x = 6 $\equiv$ 6 mod 7, I don't think these are the same though. If you look at x $\equiv$ 6 mod 7, 13 could work for that 13 isn't 6. – committedandroider Feb 13 '15 at 22:46
  • And k, 2 in this case, doesn't always have to less than the modulo number right? Cause you could have something like n $\equiv$ 7 mod 2? – committedandroider Feb 13 '15 at 23:04
  • 1
    @committedandroider I read these left to right, so "$x=6$" is the first observation, then "$x \equiv 6 \bmod 7$" is a consequence of that first observation. And yes, you don't have to have numbers less than the modular base to make an equivalence statement, but if you want to talk about an equivalence class - which $(x \bmod m)$ would normally indicate - then that is implied to be less than the base. – Joffan Feb 13 '15 at 23:11
  • What do you mean by equivalence class? – committedandroider Feb 13 '15 at 23:32
  • sorry, I meant "congruence class" which is the modular-arithmetic terminology. – Joffan Feb 14 '15 at 00:46
1

That's the squaring step in the standard method of modular exponentiation by repeated squaring

$$\!\!\!\!\!\begin{align} a^{\large n}\ {\rm mod}\ m &\,=\, b\\ \Rightarrow\ \ \ a^{\large 2n}\ {\rm mod}\ m &\,=\, b^{\large 2}\ {\rm mod}\ m\end{align}\qquad $$

The proof is easy by converting to congruences - which are more convenient arithmetically

$$\begin{array}{rrl} &a^{\large n}\ {\rm mod}\ m &\!\!=\ b\\ \Rightarrow&\ \ a^{\large n}\! &\!\!\equiv\ b\ \ \pmod m\\ \color{#c00}\Rightarrow&\ \ a^{\large 2n}\! &\!\!\equiv\ b^{\large 2} \pmod m\\ \Rightarrow&\ a^{\large 2n}\ {\rm mod}\ m &\!\!\!=\ b^{\large 2}\ \ {\rm mod}\ m\end{array}\qquad$$

where the $\rm\color{#c00}{red}$ inference employs the $ $ Congruence Power Rule for power $\,k = 2\,$ (squaring)

$$\qquad\qquad\ \ \begin{align} c &\,\equiv \, d\pmod m\\ \Rightarrow\ \ \ c^{\large k}\! &\,\equiv\, d^{\large k}\!\!\!\!\pmod m\end{align}\qquad $$

which is an inductive extension of the Congruence Product Rule $ $ (which could instead be used)

$$\qquad\qquad\ \ \begin{align} c &\,\equiv \, d\pmod m\\ \bar c &\,\equiv \, \bar d\!\pmod m\\ \Rightarrow\ \ \ c\bar c\! &\,\equiv\, d\bar d\!\!\!\!\pmod m\end{align}\qquad $$

The other inferences are standard conversions between mod as an operator and congruence, and their proofs are straightforward using the definitions.

Remark $\ $ Generally, as above, it is straightforward to prove properties of the mod operator by first converting to congruence form, then applying the arithmetical laws of congruences then, finally, converting back to operator form. While it is possible to perform such proofs without congruences, generally that will be messier, and less conceptual.

Community
  • 1
Bill Dubuque
  • 272,048
  • how did you go from $a^n$ mod m = b to $a^n \equiv$ bmod(m)? The first is saying the remainder when $a^n$ is divided by m is b. The second is saying $a^n$ - b is a multiple of m. I don't see the relationship between the two. – committedandroider Feb 13 '15 at 22:11
  • @com As I said, those are standard, e.g $\ x\ {\rm mod}\ m = r,\Rightarrow, x = r + qm,\Rightarrow, x\equiv r\pmod m\ \ $ – Bill Dubuque Feb 13 '15 at 22:14
  • Oh I remember thanks. Sorry I am really slow at this but how did you get to the next step, that is $a^{2n} \equiv b^2 (mod$ m) from $a^n \equiv $ b (mod m)? To get $a^{2n}$, what makes sense to me algebra wise is to multiply both sides by a, but then you get $a^{2n} \equiv $ ab mod(m)? – committedandroider Feb 13 '15 at 22:23
  • @com As I said, the red inference used the Power rule. – Bill Dubuque Feb 13 '15 at 22:25
  • Oh operator means modulus as an operator, meaning something like 5 mod 3 while congruence means modulus as a relationship, like 3 $\equiv$ 3mod(6)? – committedandroider Feb 13 '15 at 22:58
  • @com Right the former is a binary operation, and the latter is a ternary relation (except it is binary if we omit/fix the modulus). – Bill Dubuque Feb 13 '15 at 23:06
1

Given:

$$A \bmod n = a => A = n * k_A + a$$

and

$$B \bmod n = b => B = n * k_B + b$$

then:

$$A * B = (n * k_A + a) * (n * k_B + b)$$

$$A * B = n^{2} * k_A * k_B + n * k_A * b + n * k_B * a + a*b $$

As $k_A$, $k_B$, $a$ and $b$ are integers, the modulo operation removes every multiple of n, leaving only $a * b$

therfore:

$$(A * B) \bmod n = (a * b) \bmod n$$

Given that exponation is a multiplication, this should explain the property you were asking for

Alejo Dev
  • 111
0

The property you are asking about is why from $ab=c$ (in your concrete case with $a=5^8$, $b=5^{32}$ and $c=5^{40}$) one can deduce that $(a\bmod n)(b\bmod n)=c\bmod n$ for any positive integer $n$ (here $n=7$). Actually that is not right, since it boils down to $4\times 4=5^{40}\bmod 7$, which of course cannot be true, since $16$ is not a valid remainder modulo$~7$. What is going to be true is that the right hand side will be equal to $16\bmod 7=2$. Therefore the equation to establish should be formulated as $$ ((a\bmod n)(b\bmod n))\bmod n=(ab)\bmod n. $$ Since that makes a lot of applications of "$\bmod n$", so it is more convenient to state it using the relation $x\equiv y\pmod n$, which one may define to hold if and only if $x\bmod n=y\bmod n$. Now obviously one has in particular $a\equiv a\bmod n\pmod n$, so it will suffice to prove the more general fact $$ a\equiv a'\pmod n \text{ and } b\equiv b'\pmod n \implies ab\equiv a'b'\pmod n $$ (this is applied with $a'=a\bmod n$ and $b'=b\bmod n$). Now it is easy to see that $x\equiv y\pmod n$ if and only if $y=x+kn$ for some integer $k$. Therefore one may write $a'=a+kn$, $b'=ln$, and $$ a'b'=(a+kn)(b+ln)=ab+knb+aln+knln = ab+(kb+la+kln)n $$ from which is it clear that $a'b'\equiv ab\pmod n$, which completes the proof.

Marc van Leeuwen
  • 115,048
0

This is an elementary property of the product in modular arithmetic: $$(ab)\bmod c=(a\bmod c)(b\bmod c).$$

(More precisely, $((a\bmod c)(b\bmod c))\bmod c$ as the product can exceed $c$.)

Why is it so ?

$(a+kc)b=ab+(kb)c$: adding a multiple of $c$ to a factor adds a multiple of $c$ to the product, hence nothing changes, modulo $c$.

The same holds for addition or subtraction: $$(a\pm b)\bmod c=(a\bmod c)\pm(b\bmod c).$$

(More precisely, $((a\bmod c)\pm(b\bmod c))\bmod c$ as the sum can exceed $c$ or the difference be negative.)

  • Can you edit it so you just have the precise definition. I feel like that's more clear to readers. I try proposing an edit but I guess I don't have enough influence yet. – committedandroider Feb 13 '15 at 22:14
  • No, I presented it this way on purpose. (I think your edit was rejected because the reviewers understood my intent.) –  Feb 14 '15 at 08:15