14

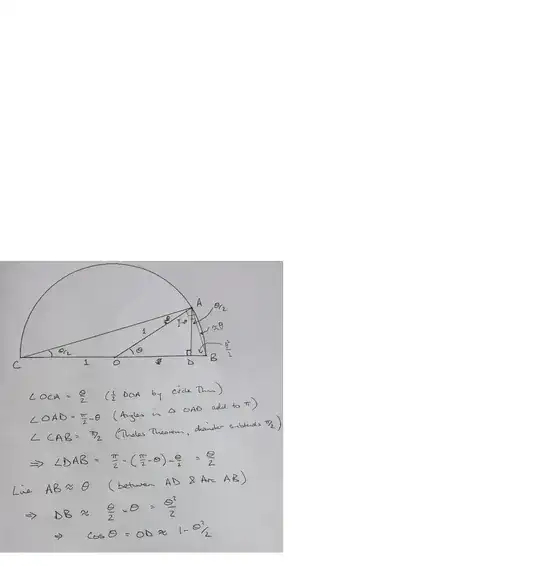
Everyone knows the picture that explains instantly the small angle approximation to the sine function (as defined by the parametrisation of the unit circle): "what's the length of that arc?" "See how for small angles, it forms the opposite side of a triangle...?"

Cosine is more problematic; the corresponding annotation on Wikipedia to the diagram mentioned above reads:

H and A are almost the same length, meaning $\cos(\theta)$ is close to $1$ and $\frac{\theta^2}{2}$ [?!] helps to trim the red away [?!].

For the syllabus I teach, students must be able to differentiate sine and cosine from first principles using the above approximations. And certainly they don't need to understand the approximations; but it would be nice, wouldn't it...

Now everyone also knows that the small angle approximation for $\cos$ is just the truncated ($O(\theta^3)$) Taylor series, and it's fairly easy to see that for small $\theta$:

$$\cos(\theta)= \sqrt{1-\sin^2(\theta)} \approx \sqrt{1- \theta^2}$$

which $\approx 1- \frac{\theta^2}{2}$ by the binomial expansion for $\sqrt{1-x}$

...But my students don't know Taylor series or binomial expansions.

Question: Can one do any better?

Asaf Karagila
  • 393,674
Tom Boardman
  • 3,505
  • And, no, drawing the graphs doesn't count. – Tom Boardman Feb 25 '12 at 23:34
  • How about completing the square and ignoring the fourth-order term in $\theta$? $\sqrt{1 - \theta^2} = \sqrt{1 - \theta^2 + \theta^4/4 - \theta^4/4} \approx \sqrt{\big(1 - \theta^2/2\big)^2}$. –  Feb 25 '12 at 23:40
  • @Tom Boardman: Does this count? $(1-\frac{x^2}{2})^2 =1-x^2+\frac{x^4}{4}\approx 1-x^2$ and therefore $\dots$. – André Nicolas Feb 25 '12 at 23:43

4 Answers4

20

You can use the double angle formula:

$$1 - \cos 2\theta = 2 \sin^2 \theta \sim 2\theta^2$$ and so

$$ \cos \theta \sim 1 - \frac{\theta^2}{2}$$

or ask them to prove that

$$\lim_{\theta \to 0} \frac{1 - \cos \theta}{\theta^2} = \frac{1}{2}$$

Aryabhata
  • 82,206
  • 1
    All of the answers here are great, but they've just learned the double angle formulae, so I'm accepting this one, as it's the one I'm probably going to teach. – Tom Boardman Feb 26 '12 at 11:02
10

One way to avoid the binomial expansion, is to note that for small $x$, $$ 1-\sqrt{1-x}=\left(1-\sqrt{1-x}\right)\frac{1+\sqrt{1-x}}{1+\sqrt{1-x}}=\frac{1-(1-x)}{1+\sqrt{1-x}}=\frac{x}{1+\sqrt{1-x}}\approx\frac{x}{2} $$ Therefore, $$ \sqrt{1-x}\approx1-\frac{x}{2} $$ Thus, for small $\theta$, $\cos(\theta)=\sqrt{1-\sin^2(\theta)}\approx1-\dfrac{\sin^2(\theta)}{2}\approx1-\dfrac{\theta^2}{2}$.

To finish things off, you can use that $\displaystyle\lim_{\theta\to0}\frac{\sin(\theta)}{\theta}=1$.

Post Script: It has been asked whether this is an over- or under-estimate.

For $x\ge0$, $\sqrt{1-x}\le1$, so we have $$ 1-\sqrt{1-x}=\frac{x}{1+\sqrt{1-x}}\ge\frac{x}{2} $$ Therefore, $$ \sqrt{1-x}\le1-\frac{x}{2} $$ Furthermore, $\sin(\theta)\le\theta$.

Thus, for small $\theta$, $\cos(\theta)=\sqrt{1-\sin^2(\theta)}\le1-\dfrac{\sin^2(\theta)}{2}\ge1-\dfrac{\theta^2}{2}$. This makes it difficult to determine that $\cos(\theta)\ge1-\dfrac{\theta^2}{2}$.

Community
  • 1
robjohn
  • 345,667
8

Do your students know the addition theorems? $\cos(\theta) = \cos^2(\theta/2)-\sin^2(\theta/2) = 1 - 2 \sin^2(\theta/2)$. Now if $\sin(\theta/2) \approx \theta/2$, you get immediately $\cos(\theta) \approx 1-\theta^2/2$.

g.castro
  • 472
  • 3
  • 8
-1

I have a graphical justification, with light use of a couple of circle theorems.

Mostly about proving that an angle = $\theta/2$, then using $\sin(\theta/2) \approx \theta/2$.

A picture is worth $10^3$ words in this case, so please look at the picture. Sketch proof of cosine small angle approximation

Ricky
  • 3,148
Tom Race
  • 1
  • @Ricky: It was a mistake to edit this post, because your edit cancelled my VLQ flag. The problem with this post, even after your edit, is that the solution is an image instead of being text, and the content of an image is not indexable and searchable. The whole point of MSE is to store only searchable content, in order for it to be easily discoverable and thus to benefit many more users in the future than just the OP. This is why we usually delete image-only posts, even when they contain correct solutions. – Alex M. Sep 13 '23 at 14:49
  • The OP asked for a graphical proof, so that's what I gave. If someone searched for "graphical proof cosine approximation" or similar, they'll find this, so is there a need to be so dogmatic about images? – Tom Race Sep 15 '23 at 09:40