Suppose that in the plane a given conic curve is compelled to pass through two fixed points of that plane.
What are the curves covered by a fixed point of the conic, its center (for an ellipse), its focus, etc. ?
(I apologize for the bad English ...)
First, a few animations:
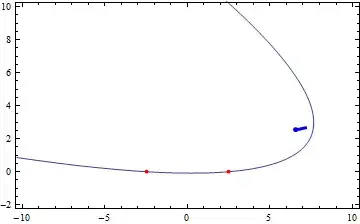
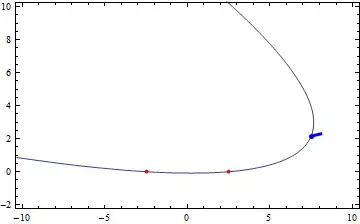
These were generated by a parabola with focal length $a=1$ and distance between two points $c=5$. The first one has the focus of the parabola as the tracing point, while the second one has the vertex as tracing point.
Now, for the mathematics: using whuber's and Blue's comments as a possible interpretation, the question is asking what would be the (point-)glissette of a conic sliding between two points. I'll consider the parabolic case here, since it's the easiest of the three.
Here's the general idea: start with some parabola $(2at\quad at^2)^T$ (where $a$ is the "focal length", or the distance from the vertex to the focus), imagine a chord of length $c$ moving along the parabola, and then translate and rotate the parabola in such a way as to have the chord's endpoints match the two fixed points at $(-c/2,0)$ and $(c/2,0)$.
Here's the complication: letting the two points on the parabola at a distance $c$ from each other have the parameters $u$ and $u+h$, we obtain the quartic equation
$$h^4+4uh^3+4(1+u^2)h^2-\left(\frac{c}{a}\right)^2=0$$
and as you might know, solving a quartic equation is complicated. The algebra is hellish, and I'll thus skip that for the time being. Assuming that we now have the (complicated!) function $h(a,c,u)$ for computing the lone positive root of that quartic equation, here's what you do: translate the tracing point $(x_t,y_t)$ so that the point $(2au\quad au^2)^T$ is the origin, rotate by an appropriate rotation matrix, and then translate again by the point $(c/2,0)$. The "appropriate matrix" is obtained by considering the slope of the chord of length $c$ of the parabola:
$$m=\frac{a(u+h)^2-au^2}{2a(u+h)-2au}=u+\frac{h(a,c,u)}{2}$$
and from that construct the rotation matrix
$$\frac1{\sqrt{1+m^2}}\begin{pmatrix}1&m\\-m&1\end{pmatrix}$$
Assembling that all together gives
$$\frac1{\sqrt{1+(u+h(a,c,u)/2)^2}}\begin{pmatrix}1&u+h(a,c,u)/2\\-u-h(a,c,u)/2&1\end{pmatrix}\cdot\left(\begin{pmatrix}x_t\\y_t\end{pmatrix}-\begin{pmatrix}2au\\au^2\end{pmatrix}\right)-\begin{pmatrix}c/2\\0\end{pmatrix}$$
You can obtain the complicated parametric equations for the parabola glissette by replacing the $h(a,c,u)$ with the appropriate expression for the positive root of the quartic equation given earlier.
The elliptic and hyperbolic cases are even more complicated than this; I'll leave the investigation of that to someone with more endurance and mathematical ability than me. :)
The Mathematica notebook for generating these animations can be obtained from me upon request.
In the Mathematica notebook I provided, I used the function Root[] for representing the function $h(a,c,u)$. To show that I wasn't pulling the leg of you, the gentle reader, I'll display the explicit form of $h(a,c,u)$, the way Ferrari would've.
Consider again the quartic equation
$$h^4+4uh^3+4(1+u^2)h^2-\left(\frac{c}{a}\right)^2=0$$
The resolvent cubic for this quartic is
$$y^3-4(u^2+1)y^2+\frac{4c^2}{a^2}y-\frac{16c^2}{a^2}=0$$
and the (only) positive root of this cubic is given by the expression
$$y_+=\frac13\left(4(1+u^2)+\frac{2(4a^2 (1+u^2)^2-3c^2)}{a\sqrt[3]{v}}+\frac{2}{a}\sqrt[3]{v}\right)$$
where
$$v=8a^3 (1+u^2)^3-9ac^2 (u^2-2)-3c\sqrt{3}\sqrt{c^4+16a^4 (1+u^2)^3+a^2 c^2 (8-20u^2-u^4)}$$
and the real cube root is always taken.
From $y_+$, we can compute $h(a,c,u)$ as the positive root of the quadratic
$$h^2+\frac{h}{2}(4u-2\sqrt{y_+-4})+\frac12\left(y_+-\sqrt{\frac{4c^2}{a^2}+y_+^2}\right)$$
that is,
$$h(a,c,u)=-u+\frac{\sqrt{y_+-4}}{2}+\sqrt{u^2-1-u\sqrt{y_+-4}-\frac{y_+}{4}+\sqrt{\frac{y_+^2}{4}+\frac{c^2}{a^2}}}$$
(I told you it was complicated... ;))
