System of equations with 2 parameters

Question

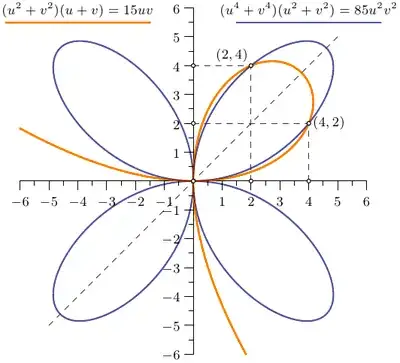
I have no idea how even to start! \begin{align*} (u^2+v^2)(u+v)&=15uv \\ (u^4+v^4)(u^2+v^2)&=85u^2v^2 \end{align*}

Answer 1

The system \begin{align} (u^2+v^2)(u+v)&=15 u v, \\ (u^4+v^4)(u^2+v^2)&=85u^2 v^2. \end{align} can be rewritten, using Newton's identities: \begin{align} p_1 & = e_1 \\ p_2 &= e_1 p_1 - 2 e_2 \\ p_3 &= e_1 p_2 - e_2 p_1 + 3 e_3 = e_1 p_2 - e_2 p_1 \\ p_4 &=e_1 p_3-e_2 p_2 + e_3 p_1 -4 e_4 = e_1 p_3-e_2 p_2 \end{align} as \begin{align} p_2 e_1&=15 e_2, \\ p_4 p_2&=85 e_2^2, \end{align} where \begin{align} p_i&=u^i+v^i, \\ e_1&=u+v,\ e_2=u v, \ e_i=0,\quad \forall i>2. \end{align}

Now we can express $p_2,p_3$ and $p_4$ in terms of $e_1$ and $e_2$ and find out that

\begin{align} e_2 = \frac{e_1^3}{2 e_1+15}. \end{align}

Then it boils down to equation in terms of $e_1$: \begin{align} e_1^4 (3e_1+35)(e_1-6)=0, \end{align} hence \begin{align} e_1&=0,6,-\frac{35}{3}; \\ e_2&=0,8,\frac{1715}{9}. \end{align}

Thus solutions to the original system are: \begin{align} (u,v)&=(0,0),(2,4),\left(\frac{-35+7i\sqrt{115}}{6},\frac{-35-7i\sqrt{115}}{6}\right), \end{align} and since the system is symmetric, we also need to include pairs $(v,u)$.

The illustration shows points of real solutions:

Answer 2

Let us try whether substituting $v=ut$ simplifies things. (Note that we take $t=v/u$, so we should check what happens for $u=0$ separately.)

The original system is then modified to: $$ \begin{align*} u(1+t^2)(1+t)&=15t^2\\ u^2(1+t^4)(1+t^2)&=85t^4 \end{align*} $$

To eliminate the variable $u$, let us divide the second equation by square of the first equation. (Again, this only works if the value of $u(1+t^2)(1+t)=15t^2$ is non-zero, so the zero case should be checked separately.) We get $$\frac{(1+t^4)(1+t^2)}{(1+t^2)^2(1+t)^2}=\frac{85t^4}{15^2t^4}$$ which can be simplified to $$45(1+t^4)=17(1+t^2)(1+t)^2.$$

---

This is a quartic equation. They might be cumbersome to do by hand, but there are various methods do solve such equations. In this case, if you were able to guess that two roots are $t=2$, $t=\frac12$ you can divide it by $(t-2)(t-1/2)$ and then you have quadratic equation. (Of course, instead of guessing you might use rational roots theorem. But this would be quite a lot of work to do by hand, considering that coefficients are not that small.)

Or you can use the fact that it is a reciprocal equation. After simplification you get $28t^4-34t^3-34t^2-34t+28$. Notice the symmetry in the coefficients.

There are special methods for solving reciprocal equations. You can find more about this type of equations under the name reciprocal equation or reciprocal polynomial. See, for example, also this post Quadratic substitution question: applying substitution $p=x+\frac1x$ to $2x^4+x^3-6x^2+x+2=0$ (And several of the posts shown there among linked questions.)

I should point out that identities used when solving reciprocal equations are similar to the corresponding identities for symmetric polynomials. So, in some sense, we could say that this answer uses similar ideas as g.kov's answer.

---

WolframAlpha returns for this equation the roots $$ \begin{align*} t&=2\\ t&=\frac12\\ t&=\frac{-9-i\sqrt{115}}{14}\\ t&=\frac{-9+i\sqrt{115}}{14} \end{align*} $$