2

What is the proof for $\forall x \in [0, \frac{\pi}{2}]\quad \sin(x) \ge \frac{x}{2}$ ?
Assuming it is true.

Dor
  • 1,074

5 Answers5

5

Well, simply study the variations of $f(x)=\sin(x)-\dfrac{x}{2}$ : compute $f'$, solve $f'(x)=0$, study the sign of $f'$ and so on...

GreginGre
  • 174
2

the graph of $y = f(x) = \sin x$ is concave down on $[0,\pi/2], $ therefore $ \sin x \ge \dfrac{2x}{\pi} > \dfrac{x}{2}$ on $0 \le x \le \pi/2.$

edit: I used that the secant line $y = 2x/\pi$ is below the graph $y = \sin x$ on the interval $0 \le x \le \pi/2$.

Martin Sleziak
  • 53,687
abel
  • 29,170
2

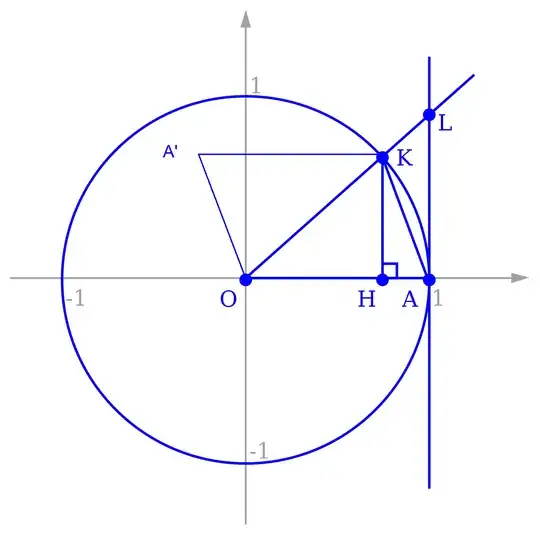
enter image description here

let $$\widehat{KOA}=x$$ the area of parallel sides kA'OA $=\sin x$

the area of Circular sector $=\frac{1}{2}x$

so you can see that the area of Circular sector < the area of parallel sides

$$\Rightarrow\sin x >\frac{1}{2}x $$

mnsh
  • 5,875
  • 3
    I think this becomes a little more obvious if we use $AK$ rather than $OK$ as the diagonal of the parallelogram, so that the parallelogram completely contains the circular sector. – David K Jan 30 '15 at 13:57
1

When $0\leq x\leq{\pi\over2}$ then $\cos{x\over2}\geq{1\over\sqrt{2}}$ and therefore $$\sin x=2\cos{x\over2}\sin{x\over2}=2\cos^2{x\over2}\tan{x\over2}\geq\tan{x\over2}\geq{x\over2}\ .$$

Christian Blatter
  • 226,825
1

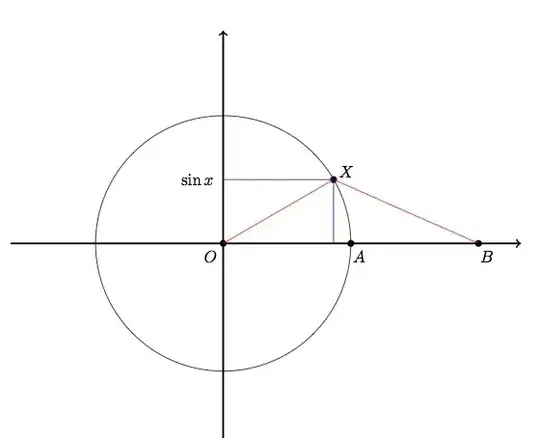
From the figure:

Arc$(AX)=x \Rightarrow $ area-sector$(OAX)=x/2$

$ AB=OA=1 \Rightarrow $ area-triangle$(OXB)= \sin x$.

So we can simply see the statement.

enter image description here

Emilio Novati
  • 62,675
  • 1
    Could you please clarify regarding area-sector$(OAX)=x/2$ ? – Dor Jan 30 '15 at 21:45
  • 1
    The area of the circle is $\pi^2r=2\pi r^2/2$. Note that $2\pi r$ is the length of the entire circumference, so, for an arc of length $x$ we have area-sector=$xr/2$, and as $r=1$... – Emilio Novati Jan 30 '15 at 22:07