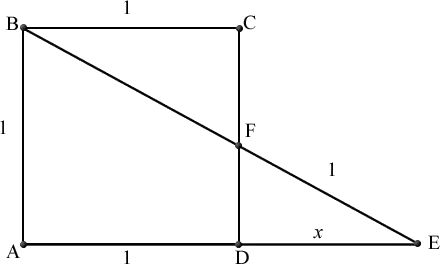
Can someone help me on this one?
I have found that $\frac{1}{(x+1)^2}+1=\frac{1}{x^2}$, but I can't solve the fourth degree equation that comes with it. There must be a easier way!

Can someone help me on this one?
I have found that $\frac{1}{(x+1)^2}+1=\frac{1}{x^2}$, but I can't solve the fourth degree equation that comes with it. There must be a easier way!
edit 1:
let $\cos{A}=x \implies \sin{A}+\tan{A}=1 \implies 1=\dfrac{1}{\sin{A}}-\dfrac{1}{\cos{A}}$
$\sin{A}\cos{A}=\cos{A}-\sin{A} \iff (\sin{A}\cos{A})^2=1-2\sin{A}\cos{A}$
let $u=\sin{A}\cos{A}\implies u^2=1-2u$
so you have one postive root $u_1$
$u_1^2=x^2(1-x^2),t=x^2>0 \implies t(1-t)=u_1^2$
now you have another positive root $t_1, x=\sqrt{t_1}$
here is partial answer:
we need to solve $(1 + \frac{1}{x})^2 = 1 + (1+x)^2$ on clearing you get the quartic $$ 0= f(x) = x^4 + 2x^3 + x^2 -2x - 1 = g(x) + h(x), \text{ where } g(x) = x^4 + x^2 - 1, h(x) = 2x^3 - 2x.$$
we are only interested in the solution $0 < x < 1.$ we can find a lower bound for $x$ this way. $g(x) = 0$ at $x^2 = \dfrac{-1+ \sqrt 5}{2}$ so the positive zero of $g$ is $\sqrt{\dfrac{-1+ \sqrt 5}{2}}$ and $h(x) < 0 \text{ on } 0< x < 1.$ by inspecting the sign of $g$ and $h$ we can conclude that the only zero of $f = g+h$ is $$\sqrt{\dfrac{-1+ \sqrt 5}{2}} < x < 1.$$