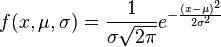
Under a normal distribution, μ = 0 and σ = 1, but when then integrating this equation, I get an error function.
Without using Riemann sums, how can I prove that this equation = 1?
I have only had a year of calc, no multivar.
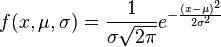
Under a normal distribution, μ = 0 and σ = 1, but when then integrating this equation, I get an error function.
Without using Riemann sums, how can I prove that this equation = 1?
I have only had a year of calc, no multivar.
This proof uses as little multivariable calculus as I can manage. Let $f$ be the standard normal distribution $$f(x)=\frac{1}{\sqrt{2\pi}}e^{-x^2/2},$$ $$\int_{-\infty}^\infty f(x)\,dx=A$$ and $$g(x,y)=f(x)f(y)=\frac{1}{2\pi}e^{-(x^2+y^2)/2}.$$
By rotational symmetry, the area under $g$ can be evaluated using shell integration in $r=\sqrt{x^2+y^2}$ and then a change of variables to $t = r^2$: $$V=\int_0^\infty 2\pi r \frac{1}{2\pi }e^{-r^2/2}dr=\int_0^\infty \tfrac{1}{2} e^{-t/2} dt = 1.$$ However it can also be evaluated using a double integral: $$\begin{align}V&=\int_{-\infty}^\infty\int_{-\infty}^\infty f(x)f(y)\,dxdy\\ &=\int_{-\infty}^\infty f(x)\,dx\cdot\int_{-\infty}^\infty f(y)\,dy\\ &=\left[\int_{-\infty}^\infty f(x)\,dx\right]^2\\ &=A^2 \end{align}$$ Since $1=V=A^2$, $A=1$. Now if $f$ is not the standard normal distribution, but another normal distribution, do the variable change $z=(x-\mu)/\sigma$. $$\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}\sigma}e^{-(x-\mu)^2/(2\sigma)^2}\,dx=\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}}e^{-z^2/2}\,dz=1$$