Consider the hexagon formed by the six points which trisect the sides of a triangle(two on each side). Is is true that when we connect opposite points in this hexagon, the lines intersect at a single point ? I think this is most likely true but I cant prove it.
3 Answers
Yes, the diagonals meet at a common point.
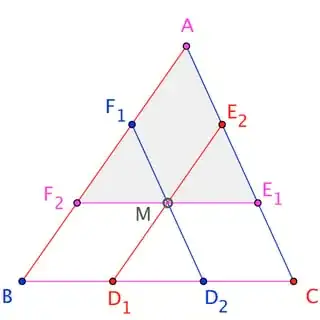
Certainly, the diagonals are parallel to, and two-thirds the length of, corresponding sides of the triangle. Consider a sub-triangle (say, $\triangle AF_2 E_1$) created by one of the diagonals and an appropriate vertex. The other diagonals ($F_1D_2$ and $E_2 D_1$) are parallel to sides ($AF_2$ and $AE_1$) of that triangle at the corresponding midpoints; those diagonals, then, necessarily meet the midpoint ($M$) of the remaining side (namely, diagonal $F_2 E_1$) at their own midpoints. $\square$
Alternatively (though less-enlighteningly), you could use my Extended Ceva's Theorem from this answer, which gives this condition for concurrence:
$$\begin{align} 1 & = \frac{|BD_1|}{|D_1C|}\;\frac{|CE_1|}{|E_1A|}\;\frac{|AF_1|}{|F_1B|} + \frac{|D_2C|}{|BD_2|}\;\frac{|E_2A|}{|CE_2|}\;\frac{|F_2B|}{|AF_2|} \\[4pt] &+\frac{|BD_1|}{|D_1C|}\;\frac{|D_2C|}{|BD_2|}+\frac{|CE_1|}{|E_1A|}\;\frac{|E_2A|}{|CE_2|}+\frac{|AF_1|}{|F_1B|}\;\frac{|F_2B|}{|AF_2|} \end{align}$$
In this situation, all ratios are $\frac12$, so the condition is satisfied and the lines are concurrent. $\square$
they do meet at the center of the triangle. to see this let we $a, b, c$ represent the points. call the points $A_1, A_2$ on $BC$ such that $BA_1 = A_1A_2 = A_2C$ the point $a_1 = 2/3 b + 1/3 c, a_2=1/3b + 2/3 c$ similarly define points $b_1=1/3 c+2/3a, b_2 = 2/3 c+ 1/3 a.$ the point where all diameters meet is mid point of $A_1B_1$ given by $(a+b+c)/3.$
- 29,170
-
How did you know that the point where all the diameters meet is the midpoint? – Bobby Jones Jan 29 '15 at 07:24
-
1the line $B_1A_1$ is parallel to $B_2A_2$ and $B_1A_1 = 2B_2A_2$ – abel Jan 29 '15 at 07:28
-
ohh I see. Thanks! – Bobby Jones Jan 29 '15 at 07:30
-
Will they meet at centroid?? – Archis Welankar Dec 06 '15 at 16:59
-
@ArchisWelankar, yes, they do meet at the centroid. – abel Dec 06 '15 at 17:05
Not too hard, borrowing the diagram above. Easy to prove triangles F1E2M and D2D1M are congruent (using similar triangles to first show F1E2||BC and F1E2=BC/3=D1D2). Thus E2M=D1M and F1M=D2M. M is the midpoint of F1D2 and E2D1. Join F2 and M. Triangles F1F2M and F1BD2 must be similar (two sides in same ratio and included angle) Using corresponding angles, F2M||BC. The same way we can show E1M||BC F2ME1 must be a straight line, so concurrency is proved.
-
Welcome to MSE. For some basic information about writing mathematics at this site see, e.g., basic help on mathjax notation, mathjax tutorial and quick reference, main meta site math tutorial and equation editing how-to. – José Carlos Santos Jul 19 '20 at 07:33