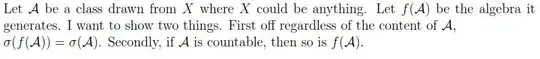
For the first question my idea was to show that $\sigma(f(\mathcal{A})) \subseteq \sigma(\mathcal{A})$ and $\sigma(\mathcal{A}) \subseteq \sigma(f(\mathcal{A}))$. As for the second question I am at a loss of what to do there. I have been tinkering with it for awhile now and have not got anywhere. Help on both questions would be much appreciated!