2

Here is what my book says about the different ways implications are worded

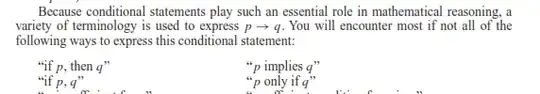
enter image description here

I am struggling with how "if p, then q" is logically equivalent to "p only if q"

The example I came up with

With "if p, then q" - If Russell plays in the NFL, he plays football.

With "p only if q" - Russell plays in the NFL only if he plays football.

Say Russell plays in the NFL, plays football and plays soccer.

With regards to that statement, my thought would be that "If Russell plays in the NFL, he plays football" implication would evaluate to true because Russell plays in the NFL and he plays football. However, with regards to "Russell plays in the NFL only if he plays football", wouldn't this evaluate to false because it says that the only way for Russell to play in the NFL is if he plays football. That means that playing football and soccer would not be a path for Russell to play in the NFL because it is not the defined only way, only playing football.

Can someone clarify this?

committedandroider
  • 1,884
  • 1
    You seem to be mixing up "only if he plays football" and "if he only plays football." In the event that he plays both, it remains the case that "he plays football" is true. – user208259 Jan 25 '15 at 06:27
  • but only if he plays football would evaluate to false right? – committedandroider Jan 25 '15 at 06:31
  • "Only if he plays football" isn't a statement that can be true or false. In a statement "$p$, only if $q$", the $p$ and $q$ are each statements, and "only if" is a connective. So when you ask whether "only if he plays football" is true, it's the same as if you asked whether "or he plays football" was true. There's an extra bit of a complete sentence that doesn't belong there. – user208259 Jan 25 '15 at 06:35
  • To me, "only if he plays football" is a statement that can be true or false. Say Russell plays football and soccer. Only if he plays football would evaluate to false because he doesn't just play football – committedandroider Jan 25 '15 at 06:38
  • No, that is part of a sentence with another part missing. It's not a complete statement on its own. – user208259 Jan 25 '15 at 06:39
  • So "only if he plays football" is the same as "or he plays football". But then that's saying p->q is logically equivalent to p v q – committedandroider Jan 25 '15 at 06:44
  • No, it's not the same in that way. What I meant is that it's meaningless for analogous reasons. – user208259 Jan 25 '15 at 06:45
  • Say I like cheese only if i like milk. I would never assess if the condition only if i like milk is ever true or false? – committedandroider Jan 25 '15 at 06:50
  • Right. "Only if I like milk" is a fragment of a sentence. It's not a statement on its own that can be true or false. – user208259 Jan 25 '15 at 06:53
  • So you can only evaluate the whole sentence or phrase, I like cheese only if i like milk. But the i like milk part would be able to be evaluated to true and false right? – committedandroider Jan 25 '15 at 06:54
  • No I don't its a duplicate because im asking "If P then Q" has the same meaning as "P only if Q", not "Q only if P" – committedandroider Jan 25 '15 at 06:56
  • @committedandroider Yes, that's right. – user208259 Jan 25 '15 at 06:56
  • So going back to that cheese example, I like cheese only if i like milk. Say I like cheese, milk, and skittles. Would this assertion still hold truth? – committedandroider Jan 25 '15 at 07:01

4 Answers4

1

Your example is a little difficult to work with because there is only one "Russell".

Let $p$ = "$x$ plays in the band" and $q$ = "$x$ is interested in music".

The statement $p \to q$ asserts that:

  • if someone plays in the band, they are interested in music
  • if someone plays in the band then they are interested in music
  • if someone plays in the band implies they are interested in music
  • someone plays in the band, only if they are interested in music

The last one is awkwardly phrased and probably easier to understand phrased the other way around:

  • Only if someone is interested in music might they play in the band.
  • Only those interested in music play in the band

Essentially the statement, and each of these attempts to phrase it in English, states that the truth extent of $p$ is entirely contained within the truth extent of $q$.

Joffan
  • 39,627
  • oh someone plays in the and and they are not interested in music, that would break the truth of the implication promise ? – committedandroider Jan 25 '15 at 06:36
  • Correct; that would be a disproof of the assertion $p\to q$ – Joffan Jan 25 '15 at 06:37
  • Here's the part where i am confused. Lets that someone plays in the band, is interested in music and loves to sing. The "if someone plays in the band, they are interested in music" implication would evaluate to true(play in band -> interested in music). However to me, "someone plays in the band only if they are interested in music" would evaluate to false because that someone is interested in music, wouldn't meet the singularity requirement of "only if they are interested in music" – committedandroider Jan 25 '15 at 06:40
  • If it said "only because...", I would agree, but we are not explicitly considering motivation in this example. It would be possible to have p and q describe motivation, of course, but then the outcome would be different. – Joffan Jan 25 '15 at 06:43
  • What do you mean by motivation in this context? – committedandroider Jan 25 '15 at 06:45
  • That appeared to be your argument; I may have misunderstood. you linked the interest in music to singing rather than instruments, but that looks at motivation for being in the band, not the simple truth or falsity of the statements. – Joffan Jan 25 '15 at 06:46
  • My motivation is that from this phrasing "someone plays in the band only if they are interested in music", the only way to ever play in the band is if someone just is interested in music. Like being interested in music and doing something else like singing would not allow that person to be apart of the band – committedandroider Jan 25 '15 at 06:52
  • Aha, I understand the issue. The usage is more like "only-if" rather than "only, if". Perhaps the intended meaning is clearer with a rearrangement: "Only if someone is interested in music do they play in the band". – Joffan Jan 25 '15 at 08:01
  • Yeah in your last example, the interest in music is emphasized. It doesn't matter if you like to sing as well. This makes a whole lot more sense. I don't understand why they phrase it as p only if q and not only if q, p – committedandroider Jan 25 '15 at 08:14
  • @committedandroider The main reason it is written in that order is so that it matches the connective order of "$p$ if $q$" (which asserts $q\to p$), so that you can write both connectives together as "$p$ if and only if $q$" to get "$p\leftrightarrow q$". Although it seems that "$p$ if $q$" is also more naturally stated as "If $p$, $q$", so one may wonder why "If and only if $p$, $q$" didn't catch on. – Mario Carneiro Jan 25 '15 at 08:45
  • I like cheese if and only if i like milk. So that would mean you can imply i like milk if I like cheese and i like cheese if i like milk? – committedandroider Jan 25 '15 at 08:48
1

"If $p$ then $q$" means
"Whenever $p$ is true, $q$ is true as well" which means
"It is impossible for $p$ to hold true while $q$ does not hold" which means
"In order for $p$ to hold true, $q$ must hold true as well" which means
"$p$ holds true only if $q$ holds true", or, for short
"$p$ only if $q$"

The_Sympathizer
  • 19,651
  • oh so if p is true when q is false, that would break the contract because you're saying the only way for p to hold true is if q holds true. If q is false, there is no way to get to p? – committedandroider Jan 25 '15 at 21:31
  • @committedandroider: Right. That's exactly correct. If $q$ could be false while $p$ held true, then the implication "$p$ only if $q$" would be broken. – The_Sympathizer Jan 25 '15 at 22:00
0

"If $p$ then $q$" is definitely not the same as "$p$ only if $q$". The latter statement has the phrase "if $q$" built into it, which could be seen as an indication that it is not the same as the former. In fact, "$p$ only if $q$" is logically equivalent to "$q$ implies $p$". I'm guessing that the textbook was misread? But if you textbook is really asserting that "$p$ then $q$" $\iff$ "$p$ only if $q$" then that textbook is wrong.

graydad
  • 14,077
  • "Only if" tends to be mentioned in textbooks mainly to help people analyze "if and only if." The conjunction "only if" is rarely used on its own. – user208259 Jan 25 '15 at 06:30
  • No that user asked about Q only if P, I am asking about p only if q – committedandroider Jan 25 '15 at 06:31
  • @committedandroider eh, you are right. But the user amWhy still gives a great answer that should help clarify any misunderstanding. – graydad Jan 25 '15 at 06:33
  • Its just if then, p implies q structure makes complete sense. All the other ones are a bit cloudy – committedandroider Jan 25 '15 at 06:42
  • @graydad No, "$p\to q$" is equivalent to "$p$ only if $q$", the textbook is not wrong. For example, $x$ is an integer only if it is real, which correctly translates $x\in\Bbb Z\to x\in\Bbb R$. – Mario Carneiro Jan 25 '15 at 08:39
0

"If $p$ then $q$" certainly seems to be logically equivalent to "$p$ only if $q$. See here and here, for example.

Glorfindel
  • 3,955
Daniel W. Farlow
  • 22,531
  • Also the thread on MSE which addresses this sort of question: http://math.stackexchange.com/questions/311192/how-does-if-p-then-q-have-the-same-meaning-as-q-only-if-p – Daniel W. Farlow Jan 25 '15 at 06:54
  • Oh so to think of it as the only way to get to p is through q. If not q, there is no way you can get to p? For "I'll stay home tomorrow only if I'm sick." If you're not sick(not q), there is no way you can get to I'll stay home(not p)? – committedandroider Jan 25 '15 at 07:00
  • In a manner of speaking, yes, "the only way to get to $p$ is through $q$". Simply in terms of linguistics, the meaning of "$p$ only if $q$" would be rather meaningless if you could actually have $p$ without $q$. The links I provided address your question well, I think, in terms of 1) linguistic usage and 2) in terms of mathematics, respectively. – Daniel W. Farlow Jan 25 '15 at 07:04
  • Yeah its weird cause when you say if p, then q. p isn't the only way to get to q. There could be plenty of other ways. – committedandroider Jan 25 '15 at 07:05
  • @committedandroider Yes, but now you've flipped it from your earlier usage. "If $p$ then $q$" and "$p$ only if $q$" both mean that "the only way to get to $p$ is through $q$". Neither one suggest that the only way to get to $q$ is through $p$ - indeed $q$ can be true and $p$ false. – Mario Carneiro Jan 25 '15 at 08:36
  • If I like cheese, I like milk. The only way to me liking cheese is me liking milk? Because if I say other than milk, I cannot get cheese because that would fall under p, not q? – committedandroider Jan 25 '15 at 08:47
  • It's not a matter of what truths you disclose, but what truths are actually true. When you say "the only way to you liking cheese is you liking milk", the meaning of this is that if you "found a way" to liking cheese by any other method, i.e. you deduce that you like cheese, the statement implies that you must also like milk. It is possibly simpler to consider universal statements such as Joffan's answer, though, since individual facts are usually known true or false (you are probably already aware whether you like cheese or not), although the logic works the same regardless. – Mario Carneiro Jan 25 '15 at 08:54
  • This does not imply that you don't also like other things, i.e. if you like meat and cheese, then the statement says you must also like milk, but does not deny the possibility of you also liking meat. So this "only way to $p$" business is just saying that $q$ is also satisfied in any world where $p$ is satisfied, not asserting that anything else is false. – Mario Carneiro Jan 25 '15 at 08:57