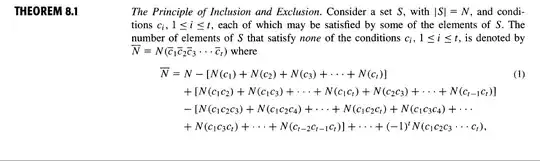A little late, but for the sake of completeness, here is the correct way to use the formula.
You're looking for $E_2$ (exactly 2 students getting nothing). Applying the formula directly, and as you already stated, you get:
$$E_2 = S_2 - \binom{3}{1}S_3 + \binom{4}{2}S_4$$
Now you need to compute $S_2$, $S_3$ and $S_4$.
Let $c_1$ be the case where student 1 gets nothing, $c_2$ the case where student 2 gets nothing, same pattern for $c_3$ and $c_4$. To apply the formula, we are interested in the cases where 2 students get nothing (for instance, $N(c_1c_2)$), the cases where 3 students get nothing (for instance, $N(c_1c_2c_3)$), and finally the cases where 4 students get nothing (that is: $N(c_1c_2c_3c_4)$
If student 1 and student 2 get nothing, that means that all prizes are given to the 2 other students: $N(c_1c_2) = 2^{10}$. Same thing for all other combinations of 2 students, and there are $\binom{4}{2}$ of them. This leads to:
$$S_2 = \binom{4}{2}2^{10}$$
If student 1, student 2 and student 3 get nothing, that means that all prizes are given to the last student: $N(c_1c_2c_3) = 1^{10}$. Same thing for all other combinations of 3 students, and there are $\binom{4}{3}$ of them:
$$S_3 = \binom{4}{3}1^{10}$$
$S_4$ counts the ways nobody gets any prize. This is not possible, as all prizes must be distributed:
$$S_4 = 0$$
Plugging that into the initial formula gives you the right answer:
$$E_2 = \binom{4}{2}2^{10} - \binom{3}{1}\binom{4}{3}1^{10} + \binom{4}{2}0 = 6132$$
By the way, turkeyhundt is right, there are of course $4^{10}$ ways to give the 10 prizes to the 4 students, not $10^4$. Even if that value is not needed here, the same reasoning is used to compute $S_2$ and $S_3$.