Fascinating induction problem with numerous interpretations

Question

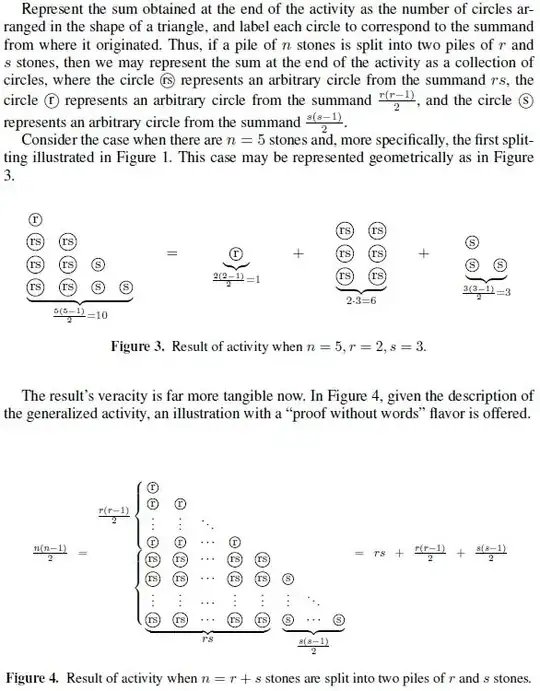
Problem: Suppose you begin with a pile of $n$ stones and split this pile into $n$ piles of one stone each by successively splitting a pile of stones into two smaller piles. Each time you split a pile, multiply the number of stones in each of the two smaller piles you form, so that if these piles have $r$ and $s$ stones in them, respectively, you compute $rs$. Once you have finished splitting the piles, calculate the sum of the products computed at each step. Does the order of how you split the piles effect the final summation?

---

Simple strong induction proof: It looks as if the sum will always be $n(n-1)/2$. Briefly, the pile of $n$ stones is split into piles of $r$ and $s=n-r$ stones, where $r$ is a positive integer less than $n$. The key inductive step for the strong induction proof is $$ rs+\frac{r(r-1)}{2}+\frac{s(s-1)}{2}=\frac{(r+s)(r+s-1)}{2}=\frac{n(n-1)}{2}. $$

---

My question: Are there any neat ways to interpret this problem and its solution?

---

This problem appears in several sources where the result is often included and you are asked to prove it using induction. I noticed that there are a number of ways to view this problem and its concomitant analogues (but I am lacking a good, intuitive geometric interpretation or analysis):

1. Combinatorics: Instead of summing the products for all of the pile splittings for $n$ stones, label the stones $1$ through $n$ and let them be elements of a set $M$. For every split, pair all of the stones in the first set with all of the stones in the second set. Every pair produced in this way appears exactly once during the activity. The terms in the sum are the number of new pairs generated after every split. Consider the power set $\mathcal{P}(M)$. By making such pairings, we have generated all distinct 2-element subsets of $\mathcal{P}(M)$.

2. Graph theory: Instead of summing the products for all of the pile splittings for $n$ stones, scatter the stones on a flat surface. Mathematically speaking, let $P_1,P_2,\ldots,P_n$ be $n$ points in a plane where no three points are collinear. Each point represents a stone or vertex. With this understanding, the situation may be modeled by a simple graph $G=(V,E)$. If we were to connect every pair of vertices with an edge for a graph $G$, that is, construct the complete graph $G=K_n$, then the number of edges for $K_n$ would be the same as the sum of the products in the original activity.

3. Combinatorics and graph theory: We can actually give a sort of restatement of the key inductive step that was used to prove the result of the activity by considering an exercise that appears in D.B. West's Introduction to Graph Theory:

$\underline{\text{Exercise:}}$ Use complete graphs and counting arguments to prove that $$ \binom{n}{2} = \binom{k}{2} + k(n-k) +\binom{n-k}{2}\quad|\quad 0\leq k\leq n. $$ Proof. Consider the complete graph $K_n$ which has $\binom{n}{2}$ edges. If we partition the vertices of $K_n$ into a set with $k$ elements and a set with $n-k$ elements, then we can count the edges as those within one block of the partition and those choosing a vertex from each. Consequently, the number of edges is given by $k(n-k)+\binom{k}{2}+\binom{n-k}{2}$.

---

I think these are some pretty cool ways to look at the original problem/activity. A geometric interpretation (or other) that added some intuition as to why the result of the activity is true would be quite nice.

Answer 1

Here's a slick geometric proof (I'll clean this diagram up later when I can draw it properly): $$ \begin{array}{lllllll} \circ \\ \circ & \circ\\ \circ & \circ & \circ\\ \bullet& \bullet& \bullet& \bullet\\ \bullet& \bullet& \bullet& \bullet& \circ\\ \bullet& \bullet& \bullet& \bullet& \circ & \circ \\ \end{array} $$ Here $n=7$, $r=4$, $s=3$. We start with an $(n-1)\times(n-1)$ right triangle (of area $\frac{n(n-1)}2$); then splitting $n$ and adding a term of form $r\times s$ corresponds to taking the rectangular chunk above out of the triangle, and the two piles of size $r$ and $s$ correspond to the two right triangles (of edge lengths $r-1$ and $s-1$) left over. Each further step of the process just corresponds to taking another rectangle (with its top right corner on the diagonal) out of what's left of the original right triangle and leaving two more right triangles (possibly empty) behind.

Answer 2

Think of it as an energy calculation with stack of chips (or coins) instead of piles of stones. A chip whose bottom side is at height $h$ has "potential energy" $h$; when it moves down to height $k$, it "releases" (as "heat" or whatever) the amount of energy $h-k$. A stack of $n$ chips starts with potential energy $0+1+2+\cdots+(n-1)=n(n-1)/2$, all of which is released by the time things are down to $n$ stacks of $1$ chips each.

When you split a pile of $r+s$ chips into two piles by taking, say $r$ chips from the top to make a new pile, each of those chips moves down by $s$ positions. This releases energy $rs$. So no matter how you go about the disassembly of the initial stack, the sum of those $rs$'s must be $n(n-1)/2$.

(I have to give credit here to Richard Guy, who told me about the problem a few years ago and gave me the hint "potential energy.")

Answer 3

regard the pile $A$ of $n$ stones as the nodes of a graph which initially has no edges. if $A$ is partitioned into two non-empty sets $B$ and $C$ add all the edges of the bipartite graph, which is a total of $|B| \cdot |C|$ edges. each of the piles $B$ and $C$ is again a graph with no edges.

suppose at some stage of the process a given pebble $p$ lies in a pile $D$. then $p$ is connected by an edge to all the pebbles in the complement of $D$, but to none of the pebbles in $D$.

at the completion of the process each stone is in a pile on its own. it is now connected to all the other nodes, a total of $n-1$ edges. since there are $n$ nodes, and each edge is associated with two nodes, the total number of edges is $\frac12 n (n-1)$.

Answer 4

Here is something I cobbled together that others may wish to see:

Any better (i.e., intuitive, etc) ways of doing it though?

Answer 5

Along the lines of an interpretation, and following the combinatorics interpretation given by OP in the original statement:

You want to conduct a round-robin tournament among $n$ players. One way to do this is to split the players into two sets of size $k$ and $n-k$ and have each player in one set play each player in the other set, for a total of $k(n-k)$ games. Then split any remaining set of size at least $2$ into two smaller sets, and have each player in each of the two smaller sets play each other. The number of games from any one splitting will be the product of the sizes of the two resulting sets. Continue in this manner.

Eventually all sets will be of size $1$, and everyone will have played everyone else; and so the total number of games will be $n\choose 2$, but it will also be the sum of products $rs$ where $r$ and $s$ are the sizes of the two sets coming from the splitting of one larger set.

You could do a similar interpretation with handshakes.

Answer 6

The splitting process induces the fundamental recurrence $$\color{green}{S_{r+s}=rs+S_r+S_s}.$$ This relation is sufficient to prove order invariance as $r$ and $s$ are chosen freely.